【题目】先化简,再求值:
( ![]() ﹣1)÷
﹣1)÷ ![]() ,其中x的值从不等式组
,其中x的值从不等式组 ![]() 的整数解中选取.
的整数解中选取.
参考答案:
【答案】解:原式= ![]()
![]()
=﹣ ![]()
![]()
= ![]() ,
,
解不等式组 ![]() 得,﹣1≤x<
得,﹣1≤x< ![]() ,
,
当x=2时,原式= ![]() =﹣2.
=﹣2.
【解析】先算括号里面的,再算除法,求出x的取值范围,选出合适的x的值代入求值即可.本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.
【考点精析】解答此题的关键在于理解一元一次不等式组的整数解的相关知识,掌握使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】任取不等式组
 的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 .
的一个整数解,则能使关于x的方程:2x+k=﹣1的解为非负数的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程2x2+x﹣a=0有两个不相等的实数根,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】当a、b满足条件a>b>0时,
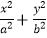 =1表示焦点在x轴上的椭圆.若
=1表示焦点在x轴上的椭圆.若 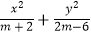 =1表示焦点在x轴上的椭圆,则m的取值范围是 .
=1表示焦点在x轴上的椭圆,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间
成人票价(元/张)
学生票价(元/张)
出发站
终点站
一等座
二等座
二等座
南靖
厦门
26
22
16
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题: ①回归直线
 恒过样本中心点
恒过样本中心点  ;
;
②“x=6”是“x2﹣5x﹣6=0”的必要不充分条件;
③“x0∈R,使得x02+2x0+3<0”的否定是“对x∈R,均有x2+2x+3>0”;
④“命题p∨q”为真命题,则“命题p∧q”也是真命题.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
相关试题

