搜索
【题目】已知am=4，an=3，则a2m+n= ．
参考答案：
【答案】48
【解析】
根据同底数幂的乘法得出a2man，根据幂的乘方得出（am）2an，代入求出即可．
解：∵am=4，an=3，
∴a2m+n=a2man=（am）2an=42×3=48，
故答案为：48．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小华用500元去购买单价为3元的一种商品，剩余的钱数y(元)与购买这种商品的件数x(件)之间的关系是__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①所示，直线L：y=m（x+10）与x轴负半轴、y轴正半轴分别交于A、B两点．
（1）当OA=OB时，试确定直线L的解析式；
（2）在（1）的条件下，如图②所示，设Q为AB延长线上一点，作直线OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=8，BN=6，求MN的长；
（3）当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图③．
问：当点B在y轴正半轴上运动时，试猜想PB的长是否为定值？若是，请求出其值；若不是，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个多边形的内角和等于外角和的3倍，求这个多边形的边数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
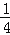x2+bx+c与x轴交于点A（﹣2，0），交y轴于点B（0，
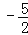）．直线y=kx
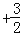过点A与y轴交于点C，与抛物线的另一个交点是D．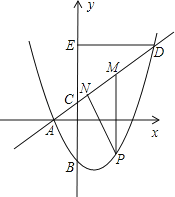
（1）求抛物线y=
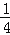x2+bx+c与直线y=kx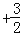的解析式；（2）设点P是直线AD下方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；
（3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为m，点P的横坐标为x，求m与x的函数关系式，并求出m的最大值．
-
科目： 来源： 题型：
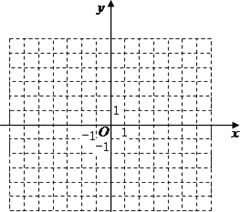
查看答案和解析>>【题目】（1）在如图所示的平面直角坐标系中表示下面各点：
A（0，3）；B（5，0）；C（3，﹣5）；D（﹣3，﹣5）；E（3，5）；
（2）A点到原点的距离是 ．
（3）将点C向x轴的负方向平移6个单位，它与点 重合．
（4）连接CE，则直线CE与y轴是什么位置关系？
（5）点D分别到x、y轴的距离是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学活动小组在一次活动中，对一个数学问题作如下探究：
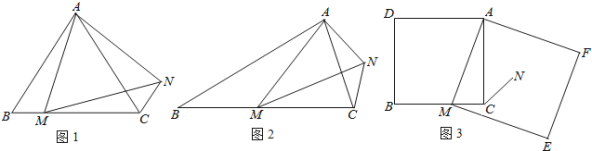
问题发现：如图1，在等边三角形ABC中，点M是边BC上任意一点，连接AM，以AM为边作等边三角形AMN，连接CN，证明：BM=CN．
变式探究：如图2，在等腰三角形ABC中，BA=BC，∠ABC=∠α，点M为边BC上任意一点，以AM为腰作等腰三角形AMN，MA=MN，使∠AMN=∠ABC，连接CN，请求出
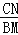的值．（用含α的式子表示出来）解决问题：如图3，在正方形ADBC中，点M为边BC上一点，以AM为边作正方形作AMEF，N为正方形AMEF的中心，连接CN，若正方形AMEF的边长为
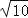，CN=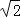
，请你求正方形ADBC的边长．
相关试题
