【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
参考答案:
【答案】(1)4ab﹣2a+![]() ;(2)b=
;(2)b=![]()
【解析】
(1)将a=﹣1,b=﹣2代入A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() ,求出A、B的值,再计算4A﹣(3A﹣2B)的值即可;(2)把(1)结果变形,根据结果与a的值无关求出b的值即可.
,求出A、B的值,再计算4A﹣(3A﹣2B)的值即可;(2)把(1)结果变形,根据结果与a的值无关求出b的值即可.
(1)4A﹣(3A﹣2B)
=4A﹣3A+2B
=A+2B,
∵A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() ,
,
∴A+2B
=2a2+3ab﹣2a﹣1+2(﹣a2+![]() ab+
ab+![]() )
)
=2a2+3ab﹣2a﹣1﹣2a2+ab+![]()
=4ab﹣2a+![]() ;
;
(2)因为4ab﹣2a+![]()
=(4b﹣2)a+![]() ,
,
又因为4ab﹣2a+![]() 的值与a的取值无关,
的值与a的取值无关,
所以4b﹣2=0,
所以b=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.

(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=10,AC=8.
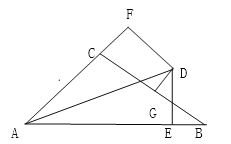
(1)求证:CF=BE;
(2) 求BE长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:“半角问题”:
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究此“半角问题”的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;(直接写结论,不需证明)
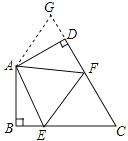
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=
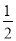 ∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=
 ∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=
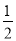 ∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2
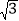 ,则AB=_____.
,则AB=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的差的绝对值等于
 ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,
,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,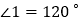 ,
,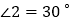 ,
,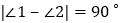 ,则
,则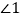 和
和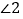 互为反余角,其中
互为反余角,其中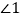 是
是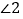 的反余角,
的反余角,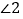 也是
也是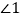 的反余角.
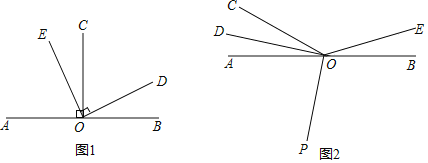
的反余角. 如图
如图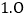 为直线AB上一点,
为直线AB上一点,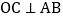 于点O,
于点O, 于点O,则
于点O,则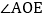 的反余角是______,
的反余角是______,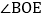 的反余角是______;
的反余角是______;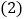 若一个角的反余角等于它的补角的
若一个角的反余角等于它的补角的 ,求这个角.
,求这个角.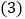 如图2,O为直线AB上一点,
如图2,O为直线AB上一点,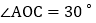 ,将
,将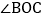 绕着点O以每秒
绕着点O以每秒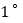 角的速度逆时针旋转得
角的速度逆时针旋转得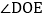 ,同时射线OP从射线OA的位置出发绕点O以每秒
,同时射线OP从射线OA的位置出发绕点O以每秒 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,
角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,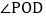 与
与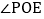 互为反余角
互为反余角 图中所指的角均为小于平角的角
图中所指的角均为小于平角的角 .
.
相关试题

