【题目】如图,∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=10,AC=8.
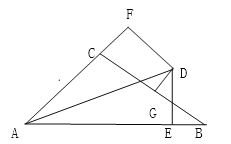
(1)求证:CF=BE;
(2) 求BE长.
参考答案:
【答案】(1)证明见解析;(2)BE=1.
【解析】
(1)连CD、BD,根据角平行线的性质定理得到DE=DF,根据线段垂直平分线的性质得到CD=BD,则可利用“HL“证明Rt△CDF≌Rt△BDE,从而得到CF=BE;
(2)先证明Rt△ADF≌Rt△ADE得到AE=AF,设BE=CF=x,则AE=10x,AF=8+x,进而列出方程求出x即可.
解:(1)连CD、BD,
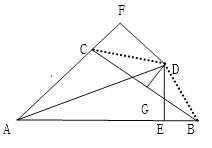
∵AD平分∠BAE,DE⊥AB,DF⊥AC,
∴DE=DF,
又∵DG垂直平分BC,
∴CD=BD,
在Rt△CDF和Rt△BDE中,![]() ,
,
∴Rt△CDF≌Rt△BDE(HL),
∴CF=BE;
(2)在Rt△ADF和Rt△ADE中,![]() ,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AE=AF,
设BE=CF=x,则AE=10x,
∵AF=AC+CF=8+x,
∴8+x=10x,
解得x=1,即BE=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
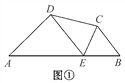
【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.
【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.
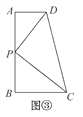
【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.
(1)请证明点P是四边形ABCD的边AB上的一个强相似点.
(2)若AD=3,BC=5,试求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2a,宽为2b的 长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形。
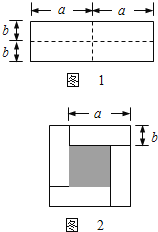
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)S阴影= ;
(方法2)S阴影= ;
(3)观察如图2,写出(a+b)2、(a-b)2,ab三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.

(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:“半角问题”:
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究此“半角问题”的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;(直接写结论,不需证明)
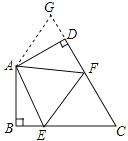
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=
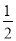 ∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=
 ∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=
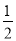 ∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+
 ab+
ab+ .
.(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2
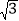 ,则AB=_____.
,则AB=_____.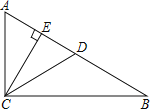
相关试题

