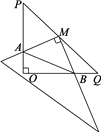
【题目】如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,∠P=∠Q=45°,将一三角尺的直角顶点放在点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明:MA=MB.
 +
+
参考答案:
【答案】说明见解析
【解析】试题分析:过点M作ME⊥PO,MF⊥QO,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得![]() 再利用“角边角”证明
再利用“角边角”证明![]() 和
和![]() 全等,根据全等三角形对应边相等即可证明;
全等,根据全等三角形对应边相等即可证明;
试题解析:过点M作ME⊥PO,MF⊥QO,
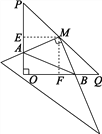
∴∠PEM=∠QFM=90°,又∵∠P=∠Q=45°,
∴∠PME=∠QMF=45°,∠EMF=90°,
又∵PM=QN,
∴△PME≌△QMF,∴EM=FM,
∵∠EMF=∠AMB=90°,
∴∠EMA=∠FMB,
又∵EM=FM,∠AEM=∠BFM=90°,
∴△AEM≌△BFM(ASA),
∴MA=MB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为160元,出售时的标价为240元,后来由于该商品积压,商店准备打折出售,但要保持利润不低于5%,则至多可打( )
A.6折
B.7折
C.8折
D.9折 -
科目: 来源: 题型:
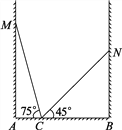
查看答案和解析>>【题目】如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:0.1252018×(-8)2019=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC -
科目: 来源: 题型:
查看答案和解析>>【题目】若|x+1|+(y﹣2)2=0,则xy的值是( )
A.﹣2
B.2
C.﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若以A(-0.5,0)、B(2,0)、C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
相关试题

