【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E,连接AG.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.

参考答案:
【答案】(1)证明见解析 (2)证明见解析
【解析】试题分析:
(1)由菱形的性质易证△ADG≌△CDG,从而可得AG=CG;
(2)由△ADG≌△CDG可得∠EAG=∠DCG,再由AB∥CD可得∠F=∠DCG,从而可得∠F=∠EAG,再利用∠AGE是公共角可证△AGE∽△FGA就可得到![]() ,所以
,所以![]()
试题解析:
(1)∵四边形ABCD是菱形,
∴AD=CD,∠ADB=∠CDB,
在△ADG与△CDG中, 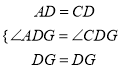 ,
,
∴△ADG≌△CDG,
∴AG=CG.
(2) ∵在菱形ABCD中,AB∥CD,
∴∠F=∠GCD.
∵△ADG≌△CDG,
∴∠EAG=∠DCG,
∴∠EAG=∠F.
又∵∠AGE=∠FGA,
∴△AGE∽△FGA,
∴![]() ,
,
∴AG2=GE·GF.
-
科目: 来源: 题型:
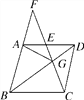
查看答案和解析>>【题目】如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D,求证:CE2=PE·DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长分别是3和6,则这个三角形的周长是( )
A. 12 B. 15 C. 12或15 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:9x2﹣81=_____.
-
科目: 来源: 题型:
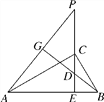
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AC的中点,ED的延长线与CB的延长线交于点F.
(1)若FD=2FB,求
 的值;
的值;(2)若AC=2
 ,BC=
,BC= ,求S△FDC的值.
,求S△FDC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据2,6,5,2,4,则这组数据的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式与x2﹣2x+1的和是2x﹣3,则这个多项式为 .
相关试题

