【题目】如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( ).
A.![]() cm
cm
B.9 cm
C.![]() cm
cm
D.![]() cm
cm
参考答案:
【答案】C
【解析】如图,圆心为A,设大正方形的边长为2x,圆的半径为R,
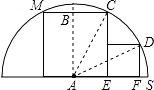
∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,
∴AE=BC=x,CE=2x;
∵小正方形的面积为16cm2,
∴小正方形的边长EF=DF=4,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+4)2+42,
解得,x=4,
∴R=4 ![]() cm,
cm,
故答案为:C.
观察图形可知正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,因此设大正方形的边长为2x,圆的半径为R,根据小正方形的面积可求出EF=DF=4,再根据R2=AE2+CE2=AF2+DF2,建立关于x的方程,求解即可得出圆的半径长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB、BC于点D、E,AP平分∠BAC,与DE的延长线交于点P.

(1)求PD的长度;
(2)连结PC,求PC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,有下列4个结论,其中正确的结论是( )
的图象如图所示,有下列4个结论,其中正确的结论是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空:
(1)(-5a4)·(-8ab2)=___.
(2)3x2y·
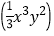 ·(5xy2)=___.
·(5xy2)=___.(3)
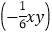 (2x-3y)=___.
(2x-3y)=___.(4)(-2ab)·(3a2-2ab-4b2)=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-3x)3·(5x2y).
(2)
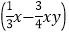 ·(-12y).
·(-12y).(3)(-4xy2)·
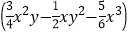 .
.(4)x3-2x
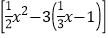 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )
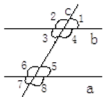
A. ①② B. ①③ C. ①④ D. ③④
相关试题

