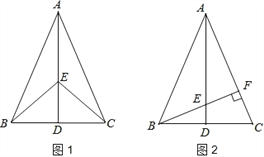
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由已知和等腰三角形的性质可得AB=AC,∠BAE=∠CAE,AE=AE,即可得到△ABE≌△ACE,应用全等三角形的性质可得BE=CE;
(2)由已知证得AF=BF,由(1)得∠EAF=∠CBF,再有∠AFE=∠BFC=90°,即可证得△AEF≌△BCF.
试题解析:证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,∵AB=AC,∠BAE=∠CAE,AE=AE,
∴△ABE≌△ACE.∴BE=CE.(运用垂直平分线的性质说明也可)
(2)∵∠BAC=45°,BF⊥AF,∴△ABF为等腰直角三角形.∴AF=BF.由(1)知AD⊥BC,∴∠EAF=∠CBF.
在△AEF和△BCF中,AF=BF,∠AFE=∠BFC=90°,∠EAF=∠CBF,
∴△AEF≌△BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
①
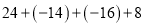 ;
; ②
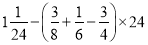 ;
;③
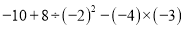 ;
; ④
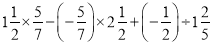 ;
;化简: ⑤
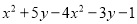 ;
; ⑥7a+3(a-3b)-2(b-3a) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-3)×2的结果是( )
A. -5 B. 1 C. -6 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根正确的是( )
A.±4
B.4
C.±8
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB和直线CD交与点O,∠BOD是它的邻补角的3倍,则直线AB与直线CD的夹角是________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面运算结果为a6的是( )
A. a3+a3 B. a8÷a2 C. a2a3 D. (﹣a2)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,若AB﹣AC=2cm,BC的垂直平分线交AB于D点,且△ACD的周长为14cm,则AB=_____,AC=_____.
相关试题

