【题目】学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.
(1)两种球拍的单价各是多少元?
(2)若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低?
参考答案:
【答案】(1)甲种球拍的单价为120元,乙种球拍的单价80元; (2)67.
【解析】分析:(1)设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,根据题意列方程即可得到结论;
(2)设购买m副甲种球拍总费用最低,总费用为y元,根据题意列不等式得到m≥![]() ,根据函数的性质即可得到结论.
,根据函数的性质即可得到结论.
本题解析:(1)设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,
根据题意得,4x=6(x﹣40),
解得:x=120,
x﹣40=80,
答:甲种球拍的单价为120元,乙种球拍的单价80元;
(2)设购买m副甲种球拍总费用最低,总费用为y元,
根据题意得,120m≥3×80,
解得:m≥![]() ,
,
∵y=120m+80=40m+8000
∵40>0,
∴当m取最小值时,总费用为y最小,
∴m=67时,总费用为y最小,
答:购买67副甲种球拍总费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的平方根是±3,3b+2的立方根是2,求a-2b的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村在开展“美丽乡村”建设时,决定购买A,B两种树苗对村里的主干道进行绿化改造,已知购买A种树苗3棵,B种树苗4棵,需要380元;购买A种树苗5棵,B种树苗2棵,需要400元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)现需购买这两种树苗共100棵,要求购买A种树苗不少于60棵,且用于购买这两种树苗的资金不超过5620元.则有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB,
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二,找出图中与AB相等的线段,并证明.
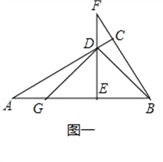

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司要设计一块面积为10平方米的正方形广告牌,公司在设计广告时,必须知道这个正方形的边长.这个正方形的边长是多少?估计边长的值(结果精确到十分位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
A.①②③④
B.④③②①
C.②④③①
D.④③①② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
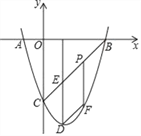
相关试题

