【题目】某校从初二(1)班和(2)班各选拔10名同学组成甲队和乙队,参加数学竞赛活动,此次竞赛共有10道选择题,答对8题(含8题)以上为优秀,两队选手答对题数统计如下:
答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数( |
甲队选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 |
乙队选手 | 0 | 0 | 4 | 3 | 2 | 1 | a |
中位数 | 众数 | 方差(s2) | 优秀率 | ||||
甲队选手 | 8 | 8 | 1.6 | 80% | |||
乙队选手 | b | c | 1.0 | m | |||
(1)上述表格中,a= ,b= ,c= ,m= .
(2)请根据平均数和众数的意义,对甲、乙两队选手进行评价.
参考答案:
【答案】(1)8,8,7,![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据表格中的数据可以求得a、b、c、m的值;
(2)根据表格中的数据可以从平均数和众数的意义,对甲、乙两队选手进行评价.
解:(1)平均数![]() .
.
中位数:共有10名同学,中位数为第5、第6的平均数,即b=8;
众数c=7,优秀率![]() ;
;
(2)甲乙两队的平均数都为8,说明两队的平均水平相同,甲队的众数为8,乙队的众数为7,说明出现人数最多的题数中,甲队大于乙队,若仅从平均数和众数分析,甲队优于乙队。
-
科目: 来源: 题型:
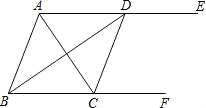
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值. -
科目: 来源: 题型:
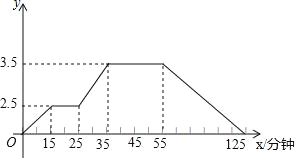
查看答案和解析>>【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800
1600
B地区
1600
1200
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内:
﹣5,|-
 |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AC=16,则图中长度为8的线段有( )

A. 2条 B. 4条 C. 5条 D. 6条
相关试题

