【题目】如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
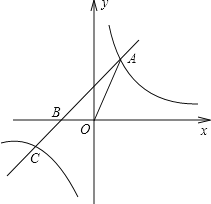
(1)求双曲线的解析式;
(2)求B点的坐标;
(3)若S△AOB=2,求A点的坐标;
(4)在(3)的条件下,在x轴上是否存在点P,使△AOP是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)B(﹣2,0)(3)A(2,2)(4)P1(2,0),P2(4,0),P3(﹣2
(2)B(﹣2,0)(3)A(2,2)(4)P1(2,0),P2(4,0),P3(﹣2![]() ,0),P4(2
,0),P4(2![]() ,0)
,0)
【解析】
试题分析:(1)根据双曲线函数的定义可以确定m的值;
(2)利用y=kx+2k当y=0时,x=2就知道B的坐标;
(3)根据(1)知道OB=2,而S△AOB=2,利用它们可以求出A的坐标;
(4)存在点P,使△AOP是等腰三角形.只是确定P坐标时,题目没有说明谁是腰,是底,所以要分类讨论,不要漏解.
解:(1)∵y=(m+5)x2m+1是双曲线
∴![]() .
.
∴m=﹣1(2分)
∴![]() (3分)
(3分)
(2)∵直线y=kx+2k(k≠0)与x轴交于点B
∴当y=0时,0=kx+2k
∴x=﹣2(5分)
∴B(﹣2,0)(6分)
(3)∵B(﹣2,0)
∴OB=2(7分)
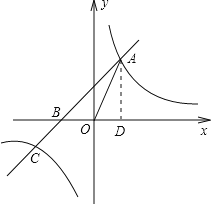
过A作AD⊥x轴于点D
∵点A在双曲线y=![]() 上,
上,
∴设A(a,b)
∴ab=4,AD=b(8分)
又∵S△AOB=![]() OBAD=
OBAD=![]() ×2b=2
×2b=2
∴b=2(9分)
∴a=2,
∴A(2,2)(10分)
(4)P1(2,0),P2(4,0),P3(﹣2![]() ,0),P4(2
,0),P4(2![]() ,0).
,0).
(写对一个得一分)(14分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
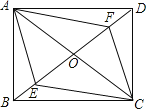
(1)求证:四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是什么特殊四边形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
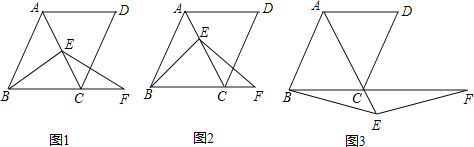
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】西北某地区为改造沙漠,决定从2012年起进行“治沙种草”,把沙漠地变为草地,并出台了一项激励措施:在“治沙种草”的过程中,每一年新增草地面积达到10亩的农户,当年都可得到生活补贴费1500元,且每超出一亩,政府还给予每亩a元的奖励.另外,经治沙种草后的土地从下一年起,平均每亩每年可有b元的种草收入.下表是某农户在头两年通过“治沙种草”每年获得的总收入情况:
(注:年总收入=生活补贴费+政府奖励费+种草收入)
年份
新增草地亩数
年总收入
2012
20
2600
2013
26
5060
年份
新增草地的亩数
年总收入
2012年
20亩
2600元
2013年
26亩
5060元
(1)试根据提供的资料确定a、b的值;
(2)观察数据,2013的新增草地的亩数在2012年新增草地的亩数上增加了一个百分数,若从2013年起,该农户每年新增草地的亩数均能比前一年按这个百分数增长,那么2015年该农户通过“治沙种草” 获得的年总收入将达到多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示﹣5 670 000时,应为( )
A.﹣567×104
B.﹣5.67×106
C.﹣5.67×107
D.﹣5.67×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为 .
相关试题

