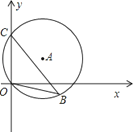
【题目】如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】试题分析:连接CD,由∠COD为直角,根据90°的圆周角所对的弦为直径,可得出CD为圆A的直径,再利用同弧所对的圆周角相等得到∠CBO=∠CDO,在直角三角形OCD中,由CD及OC的长,利用勾股定理求出OD的长,然后利用余弦函数定义求出cos∠CDO的值,即为cos∠CBO的值.
连接CD,如图所示:
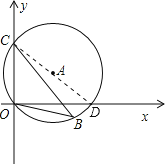
∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为![]() 所对的圆周角,
所对的圆周角,
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:![]()
∴![]() .
.
故选B
考点: 1.圆周角定理;2.勾股定理;3.锐角三角函数的定义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.正方形的周长C随着边长x的变化而变化
C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t(min)的变化而变化
D.面积为20的三角形的一边a随着这边上的高h的变化而变化 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.

①∵ ∠B=∠3(已知),∴______∥______.(______,______)
②∵∠1=∠D (已知),∴______∥______.(______,______)
③∵∠2=∠A (已知),∴______∥______.(______,______)
④∵∠B+∠BCE=180° (已知),∴______∥______.(______,______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论: ⑴小明说:y与x之间的函数关系为y=6.4x+16
⑵小刚说:y与x之间的函数关系为y=8x
⑶小聪说:y与x之间的函数关系在0≤x≤10时,y=8x;在x>10时,y=6.4x+16
⑷小斌说:我认为用下面的列表法也能表示它们之间的关系购买量/本
1
2
3
4
…
9
10
11
12
…
付款金额/元
8
16
24
32
…
72
80
86.4
92.8
…
⑸小志补充说:如图所示的图象也能表示它们之间的关系.
其中,表示函数关系正确的个数有( )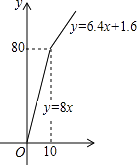
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(2)

(1)如果∠1=∠D,那么______∥________;
(2)如果∠1=∠B,那么______∥________;
(3)如果∠A+∠B=180,那么______∥________;
(4)如果∠A+∠D=180,那么______∥________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个互为相反数的有理数相除,商为( )
A.正数
B.负数
C.不存在
D.负数或不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

