【题目】为丰富学生的课余生活,陶冶学生的情操,促进学生全面发展,某中学七年级开展了学生社团活动,学校为了解学生参加情况,对部分学生进行了调查,制作出如下的统计图:

请根据统计图,完成以下问题:
(1)这次共调查了 名学生;在扇形统计图中,表示“书法类”所在扇形的圆心角是 度.
(2)请把统计图1 补充完整.
(3)若七年级共有学生1100 名,请估算有多少名学生参加文学类社团.
参考答案:
【答案】(1)50;72;(2)详见解析;(3)330.
【解析】
(1)结合两个统计图,根据体育类20人所占的百分比是40%,进行计算;根据条形统计图中书法类的人数求得所占的百分比,再进一步求得其所占的圆心角的度数;
(2)根据总人数,求得艺术类的人数补全条形统计图;
(3)求出文学类所占的百分比,再用1100乘以百分比估计即可.
(1)20÷40%=50;
10÷50×360°=72°;
(2)如图,50﹣20﹣10﹣15=5;

(3)因为![]() 1100=330.
1100=330.
所以估计有330名学生参加文学类社团.
-
科目: 来源: 题型:
查看答案和解析>>【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9,10环的子弹数因被墨水污染而看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发):
甲

乙

(1)求甲同学在这次测验中平均每发射中的环数;
(2)根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.(结果保留到小数点后1位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=﹣2x+b的图象与x轴、y轴分别交于B,A两点,与反比例函数y=
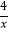 (x>0)交于C,D两点.
(x>0)交于C,D两点.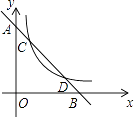
(1)若点D的坐标为(2,m),则m= , b=;
(2)在(1)的条件下,通过计算判断AC与BD的数量关系;
(3)若在一次函数y=﹣2x+b与反比例函数y=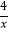 (x>0)的图象第一象限始终有两个交点的前提下,不论b为何值,(2)中AC与BD的数量关系是否恒成立?试说明理由.
(x>0)的图象第一象限始终有两个交点的前提下,不论b为何值,(2)中AC与BD的数量关系是否恒成立?试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用钉子把木棒AB,BC和CD分别在端点B,C处连接起来,AB,CD可以转动,用橡皮筋把AD连接起来,设橡皮筋AD的长是x cm.
(1)若AB=5 cm,CD=3 cm,BC=11 cm,求x的最大值和最小值;
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?

相关试题

