【题目】已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°. 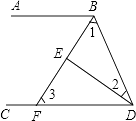
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.
参考答案:
【答案】
(1)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1= ![]() ∠ABD,∠2=
∠ABD,∠2= ![]() ∠BDC;
∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
(2)解:∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
【解析】(1)已知BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根据同旁内角互补,可得两直线平行.(2)已知∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,将等角代换,即可得出∠3与∠2的数量关系.
【考点精析】关于本题考查的角的平分线和平行线的判定,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
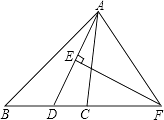
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知样本x1、x2,…,xn的方差是2,则样本3x1+2,3x2+2,…,3xn+2的方差是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产1件A种产品需甲种原料9千克,乙种原料3千克,可获利700元;生产1件B种产品需甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品可获总利润是y元,其中A种产品的生产件数是x.
(1)写出y与x之间的函数关系式;
(2)符合题意的生产方案有几种?请你帮忙设计出来;
(3)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列不等式中正确的是( )
A.a﹣b<0
B.﹣5a<﹣5b
C.a+8<b﹣8
D.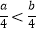
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组:
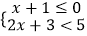 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.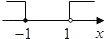
B.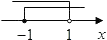
C.
D.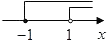
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
相关试题

