【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

参考答案:
【答案】(1)不公平,理由详见解析;(2)详见解析.
【解析】试题分析:(1)分别计算出阴影部分面积和非阴影部分面积,小红胜的概率=S阴影÷S总,小明胜的概率=S非阴影÷S总,则比较阴影部分和小圆面积即可知道是否公平;(2)用一正方形将不规则图形包围起来,根据用频率估计概率来设计.
解:(1)不公平,理由:
根据几何概率的求法:掷中阴影小红胜的概率就是阴影区域的面积与总面积的比值;小明胜的概率为小圆面积与总面积的比值,
而计算可得大圆面积为9π,小圆面积为4π.则阴影部分面积为5π,
则阴影部分面积比小圆面积大.
则小红胜的概率大于小明胜的概率,
所以该游戏是不公平的,对小红有利;
(2)能利用频率估计概率的实验方法估算非规则图形的面积.
设计方案:①设计一个面积为S的正方形将非规则图形围起来,如图:
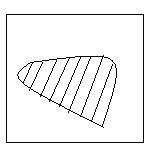
②蒙上眼在一定距离外向正方形内掷小石子,掷在正方形外不作记录;
③掷的次数充分大,记录并统计结果,其中掷入正方形内m次,n次掷非规则图形内;
④设非规则图形的面积为S1,用频率估计概率,即频率P(掷入非规则图形内)=![]() ≈概率P(掷入非规则图形内)=
≈概率P(掷入非规则图形内)=![]() ,解得S1≈
,解得S1≈![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
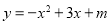 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工
管理人员
普通工作人员
人员结构
总经理
部门经理
科研人员
销售人员
高级技工
中级技工
勤杂工
员工数(名)
1
3
2
3
24
1
每人月工资(元)
21000
8400
2025
2200
1800
1600
950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资
 (结果保留整数),并判断
(结果保留整数),并判断 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】龙人文教用品商店欲购进
 、
、 两种笔记本,用160元购进的
两种笔记本,用160元购进的 种笔记本与用240元购进的
种笔记本与用240元购进的 种笔记本数量相同,每本
种笔记本数量相同,每本 种笔记本的进价比每本
种笔记本的进价比每本 种笔记本的进价贵10元.
种笔记本的进价贵10元.(1)求
 、
、 两种笔记本每本的进价分别为多少元?
两种笔记本每本的进价分别为多少元?(2)若该商店准备购进
 、
、 两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进
两种笔记本共100本,且购买这两种笔记本的总价不超过2650元,则至少购进 种笔记本多少本?
种笔记本多少本? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩“石头、剪刀、布”的游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“石头”、“剪刀”、“布”的卡片张数分别为3、5、7.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种卡片不分胜负
(1)若甲先摸,则他摸出“石头”的概率是______;
(2)若甲先摸出“石头”,则乙再摸出“石头”的概率是______;
(3)若甲先摸出了“石头”,则乙获胜的概率是______;
(4)若甲先摸,则他摸出哪种卡片获胜的可能性最大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:
 =1.73,
=1.73, =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, ,点
,点 为
为 边上一点,连接BD,点
边上一点,连接BD,点 为
为 上一点,连接
上一点,连接 ,
, ,过点
,过点 作
作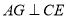 ,垂足为
,垂足为 ,交
,交 于点
于点 .
.(1)求证:
 ;
;(2)如图2,若
 ,点
,点 为
为 的中点,求证:
的中点,求证: ;
;(3)在(2)的条件下,如图3,若
 ,求线段
,求线段 的长.
的长.
相关试题

