【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需 ![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需 ![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围); 表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 | 2800 | ||
精加工获利/元 | 25800 |
y与x的函数关系式
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
参考答案:
【答案】
(1)43;50﹣x;1200;28200;400x;600(50﹣x);y=﹣200x+30000
(2)解:设应把x吨进行粗加工,其余进行精加工,由题意可得
![]() ,
,
解得,x≥30,
∵y=﹣200x+30000,
∴当x=30时,y取得最大值,此时y=24000,
即应把30吨进行粗加工,另外20吨进行精加工,这样才能获得最大利润,最大利润为24000元
【解析】(1)由题意可得, 当x=7时,50﹣x=43,
当x=3时,粗加工获利为:(4000﹣600﹣3000)×3=1200,精加工获利为:(4500﹣3000﹣900)×47=28200,
故答案为:43、50﹣x;1200、28200,400x、600(50﹣x);
y与x的函数关系式是:y=400x+600(50﹣x)=﹣200x+30000,
即y与x的函数关系式是y=﹣200x+30000;
(1)根据题意可以将表格中的数据补充完整,并求出y与x的函数关系式;(2)根据(1)中的答案和题意可以列出相应的不等式,从而可以解答本题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
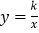 的图像经过点
的图像经过点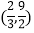 .
.(1)求k的值,并判断点
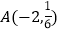 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当
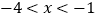 时,求y的取值范围.
时,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
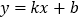 的图像与反比例函数
的图像与反比例函数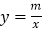 的图像交于点
的图像交于点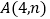 和点
和点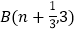 ,与
,与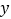 轴交于点
轴交于点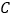 .
.(1)求反比例函数和一次函数的表达式.
(2)若在
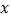 轴上有一点
轴上有一点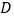 ,其横坐标是1,连接
,其横坐标是1,连接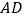 、
、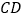 ,求
,求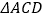 的面积.
的面积.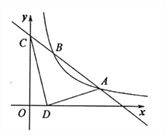
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一应用题:“李老师存了一个两年的定期储蓄5000元,到期后扣除20%的利息税能取5176元,求这种储蓄的年利率是多少?”四位同学都是设这种储蓄的年利率是x,可他们列出的方程却不同,下列列出的方程中正确的是()
A. 5000(1+x×2×20%)=5176 B. 5000(1+2x)×80%=5176
C. 5000+5000x×2×80%=5176 D. 5000+5000x×80%=5176
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个老太太提着一个篮子去卖鸡蛋,第一个人买走了她的鸡蛋的一半又半个;第二个人买走了剩下的一半又半个;第三人买走了前两个人剩下的一半又半个,正好卖完全部鸡蛋,问老太太一共卖了多少个鸡蛋.
相关试题

