【题目】如图,![]() ABCD,四个内角平分线相交于E、F、G、H。求证:四边形EFGH是矩形。
ABCD,四个内角平分线相交于E、F、G、H。求证:四边形EFGH是矩形。

参考答案:
【答案】见解析
【解析】
试题根据平行四边形的性质可得AB∥CD,AD∥BC,∠BAD+∠CDA=180°,∠ABC+∠DCB=180°,∠ADC+∠BCD=180°,又因为AE,BG,DE,FG分别为∠BAD,∠ABC,∠CDA,∠BCD的角平分线,可得∠E=180°-(∠EAD+∠EDA)=180°-![]() (∠BAD+∠CDA)=180°-90°=90°同理∠G=90°,∠GHE=∠CHD=90°,根据有三个角为直角的四边形是矩形可得证.
(∠BAD+∠CDA)=180°-90°=90°同理∠G=90°,∠GHE=∠CHD=90°,根据有三个角为直角的四边形是矩形可得证.
试题解析:∵四边形ABCD为平行四边形
∴AB∥CD,AD∥BC
∴∠BAD+∠CDA=180°,
∠ABC+∠DCB=180°,
∠ADC+∠BCD=180°
∵AE,BG,DE,FG分别为
∠BAD,∠ABC,∠CDA,∠BCD的角平分线
∴∠E=180°-(∠EAD+∠EDA)
=180°-![]() (∠BAD+∠CDA)
(∠BAD+∠CDA)
=180°-90°=90°
同理∠G=90°,∠GHE=∠CHD=90°
∴四边形EFGH为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是______形,根据的数学原理是:_______________________;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是_______形,根据的数学原理是:_____________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AB=CD,BC=AD,E、F是对角线AC上两点,且AE=CF.求证:BE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,AB=20cm,BC=4cm,点P从点A开始沿折线ABCD以4cm/s的速度运动,点Q从点C开始沿CD边以1cm/s的速度运动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts,则t为何值时,四边形APQD是矩形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要把残破的轮片复制完整,已知弧上的三点A、B、C.
①用尺规作图法找出
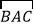 所在圆的圆心(保留作图痕迹,不写作法);
所在圆的圆心(保留作图痕迹,不写作法);②设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕着点B顺时针旋转角a(0°<a<90°)得到△A1BC;A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论.
(2)如图2,当a=30°时,试判断四边形BC1DA的形状,并证明.
(3)在(2)的条件下,求线段DE的长度.

相关试题

