搜索
【题目】如图所示，在矩形ABCD中，AB＝20cm，BC＝4cm，点P从点A开始沿折线ABCD以4cm/s的速度运动，点Q从点C开始沿CD边以1cm/s的速度运动，如果点P，Q分别从点A，C同时出发，当其中一点到达点D时，另一点也随之停止运动，设运动时间为ts，则t为何值时，四边形APQD是矩形？
参考答案：
【答案】当t＝4时，四边形APQD是矩形．
【解析】
四边形APQD为矩形，也就是AP=DQ，分别用含t的代数式表示，解即可.
解：观察图形，当AP＝DQ时，由AP∥DQ，∠A＝90°，可得四边形APQD是矩形．
∵AP∥DQ，∠A＝90°，∴当AP＝DQ时，四边形APQD是矩形．
依题意有4t＝20－t，∴t＝4，
故当t＝4时，四边形APQD是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在四边形ABCD中，AB=CD，BC=AD，E、F是对角线AC上两点，且AE=CF.求证：BE=DF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
ABCD，四个内角平分线相交于E、F、G、H。求证：四边形EFGH是矩形。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，要把残破的轮片复制完整，已知弧上的三点A、B、C.
①用尺规作图法找出
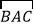所在圆的圆心(保留作图痕迹，不写作法)；②设△ABC是等腰三角形，底边BC＝8cm，腰AB＝5cm，求圆片的半径R.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕着点B顺时针旋转角a（0°＜a＜90°）得到△A1BC；A1B交AC于点E，A1C1分别交AC、BC于D、F两点．
（1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论．
（2）如图2，当a=30°时，试判断四边形BC1DA的形状，并证明．
（3）在（2）的条件下，求线段DE的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度后，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为（ ）
A．4，30° B．2，60° C．1，30° D．3，60°
相关试题
