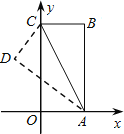
【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置.若点B的坐标为(2,4),则点D的横坐标是___________.
参考答案:
【答案】![]()
【解析】
首先过点D作DF⊥OA于F,过D作DG⊥y轴于G.由四边形OABC是矩形与折叠的性质,易证得△AEC是等腰三角形,然后在Rt△AEO中,利用勾股定理求得AE,OE的长,从而得到DE、EC的长.在Rt△EDC中,利用三角形面积公式求得DG的长,即可得点D的横坐标.
过点D作DF⊥OA于F,过D作DG⊥y轴于G.
∵四边形OABC是矩形,∴OC∥AB,∴∠ECA=∠CAB,根据题意得:∠CAB=∠CAD,∠CDA=∠B=90°,∴∠ECA=∠EAC,∴EC=EA.
∵B(2,4),∴AD=AB=4,DC=CB=2.设OE=x,则AE=EC=OC﹣OE=4﹣x.在Rt△AOE中,AE2=OE2+OA2,即(4﹣x)2=x2+4,解得:x![]() ,∴OE
,∴OE![]() ,EC=AE
,EC=AE![]() ,∴DE=DA-AE=4-
,∴DE=DA-AE=4-![]() =
=![]() .在Rt△EDC中,∵
.在Rt△EDC中,∵![]() DEDC=
DEDC=![]() DGEC,∴DG=
DGEC,∴DG=![]() =
=![]() =
=![]() ,∴点D的横坐标为:
,∴点D的横坐标为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
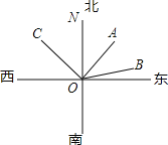
(1)求∠BOC的度数;
(2)求∠AOB的度数.
-
科目: 来源: 题型:
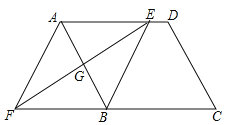
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
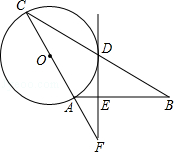
(1)求证:EF⊥AB;
(2)若∠C=30°,EF=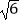 ,求EB的长.
,求EB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.

(1)在网格的格点中,以AB为边画一个△ABC,使三角形另外两边长为
 、
、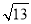 ;
;(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有 个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
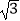 ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: 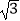 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)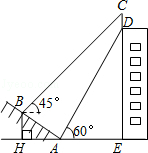
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: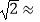 1.414,
1.414, 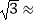 1.732)
1.732)
相关试题

