搜索
【题目】如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB=DE，此时恰有∠ADE=
∠ACB，则∠B的度数是 
参考答案：
【答案】20°
【解析】解：设∠B=x．
∵DB=DE，
∴∠DEB=∠B=x，
∴∠ADE=∠DEB+∠B=2x，
∴∠ACB=2∠ADE=4x．
∵AB=BC，
∴∠ACB=∠A=4x．
在△ABC中，∵∠A+∠B+∠C=180°，
∴4x+x+4x=180°，
∴x=20°．
即∠B的度数是20°．
故答案为20°．
设∠B=x．先由DB=DE，根据等边对等角得出∠DEB=∠B=x，根据三角形外角的性质得出∠ADE=∠DEB+∠B=2x，由∠ADE=
∠ACB得出∠ACB=4x．再由AB=BC，得出∠ACB=∠A=4x，然后在△ABC中，根据三角形内角和定理列出方程4x+x+4x=180°，解方程即可求出∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数的图象与反比例函数的图象交于点A﹙﹣2，﹣5﹚，C﹙5，n)，交y轴于点B，交x轴于点D
（1）求反比例函数
和一次函数y=kx+b的表达式；（2）连接OA，OC．求△AOC的面积；
（3）直接写kx+b＞
的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店有两种进价不同的计算机都卖了64元，其中一个赢利60%，另一个亏本20%，在这次买卖中这家商店（ ）
A. 不赔不赚 B. 赚了8元 C. 赔了8元 D. 赚了32元
-
科目： 来源： 题型：
查看答案和解析>>【题目】把几个数用大括号围起来，中间用逗号断开，如：{1，2，﹣3}、{﹣2，7，
，19}，我们称之为集合，其中的数称其为集合的元素，一个给定集合中的元素是互不相同的．
（1）类比有理数加法运算，集合也可以“相加”．定义：集合A与集合B中的所有元素组成的集合称为集合A与集合B的和，记为A+B．如A={2，﹣1}，B={﹣1，4}，则A+B={2，﹣1，4}．现在A={﹣2，0，1，5，7}，B={﹣3，0，1，3，5}，则A+B= ．
（2）如果一个集合满足：当有理数a是集合的元素时，有理数6﹣a也必是这个集合的元素，这样的集合我们称为好的集合．
①请你判断集合{1，2}，{﹣2，1，3，5，8}是不是好的集合？
②请你写出满足条件的两个好的集合的例子． -
科目： 来源： 题型：
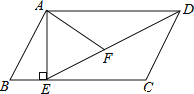
查看答案和解析>>【题目】如图，在平行四边形ABCD中，过点A作AE垂直BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某人去水果批发市场采购苹果，他看中了A、B两家苹果．这两家苹果品质都一样，零售价都为6元/千克，但批发价各不相同． A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．
B家的规定如表：数量范围（千克）
0～500
500以上～1500
1500以上～2500
2500以上
价 格（元）
零售价的95%
零售价的85%
零售价的75%
零售价的70%
【表格说明：批发价格分段计算，如：某人批发苹果2100千克，则总费用=6×95%×500+6×85%×1000+6×75%×（2100﹣1500）】
根据上述信息，请解答下列问题：
（1）如果他批发1000千克苹果，则他在A 家批发需要元，在B家批发需要元；
（2）如果他批发x千克苹果（1500＜x＜2000），则他在A 家批发需要元，在B家批发需要元（用含x的代数式表示）；
（3）现在他要批发不超过1000千克苹果，你能帮助他选择在哪家批发更优惠吗？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】90°-27°32′42″=____________________.
相关试题
