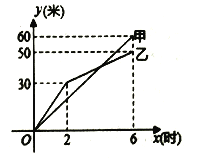
【题目】甲、乙两个工程队同时挖掘两段长度相等的隧道,如图是甲、乙两队挖掘隧道长度![]() (米)与挖掘时间
(米)与挖掘时间![]() (时)之间关系的部分图象.请解答下列问题:
(时)之间关系的部分图象.请解答下列问题:
![]() 在前
在前![]() 小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
小时的挖掘中,甲队的挖掘速度为 米/小时,乙队的挖掘速度为 米/小时.
![]() ①当
①当![]() 时,求出
时,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②开挖几小时后,两工程队挖掘隧道长度相差![]() 米?
米?
参考答案:
【答案】(1)10;15; (2) ①![]() ;②挖掘
;②挖掘![]() 小时或
小时或![]() 小时或
小时或![]() 小时后两工程队相距5米.
小时后两工程队相距5米.
【解析】
(1)分别根据速度=路程除以时间列式计算即可得解;
(2)①设![]() 然后利用待定系数法求一次函数解析式解答即可;
然后利用待定系数法求一次函数解析式解答即可;
②求出甲队的函数解析式,然后根据![]() 列出方程求解即可.
列出方程求解即可.
![]() 甲队:
甲队:![]() 米/小时,
米/小时,
乙队:![]() 米/小时:
米/小时:
故答案为:10,15;
![]() ①当
①当![]() 时,设
时,设![]() ,
,
则![]() ,
,
解得![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
②易求得:当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ;当
;当![]() 时
时![]() ,
,
由![]() 解得
解得![]() ,
,
1° 当![]() ,
, ![]() ,解得:
,解得:![]() ,
,
2°当![]() ,
,![]()
解得:![]() ,
,
3°当![]() ,
,![]() ,
,
解得: ![]()
答:挖掘![]() 小时或
小时或![]() 小时或
小时或![]() 小时后,两工程队相距
小时后,两工程队相距![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形
 中,
中, ,点
,点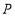 从
从 点出发,沿折线
点出发,沿折线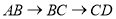 运动,到点
运动,到点 时停止,已知
时停止,已知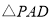 的面积
的面积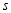 与点
与点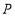 运动的路程
运动的路程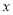 的函数图象如图②所示,则点
的函数图象如图②所示,则点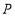 从开始到停止运动的总路程为________.
从开始到停止运动的总路程为________.
-
科目: 来源: 题型:
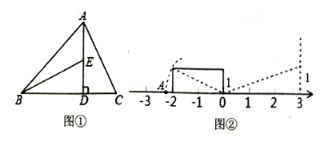
查看答案和解析>>【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
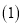 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为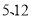 ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____;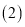 如图①,
如图①,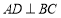 于
于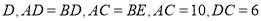 ,求
,求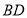 的长度;
的长度; 如图②,点
如图②,点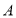 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数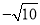 的
的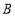 点(保留痕迹).
点(保留痕迹). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( ).
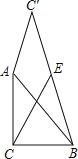
A.
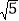 B.
B. 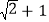 C.
C. 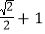 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A.
 B. 2 C.
B. 2 C.  D. 3
D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的对角线交于点O,已知△OBC的周长为59厘米,且AD的长是28厘米,两对角线的差为14厘米,那么较长的一条对角线长是______厘米.
相关试题

