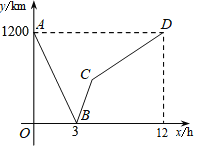
【题目】一列高铁列车从甲地匀速驶往乙地,一列特快列车从乙地匀速驶往甲地,两车同时出发,设特快列车行驶的时间为x(单位:时),特快列车与高铁列车之间的距离为y(单位:千米),y与x之间的函数关系如图所示,则图中线段CD所表示的y与x之间的函数关系式是_____.
参考答案:
【答案】y=100x![]()
【解析】
由函数图象可以直接得出甲、乙两地之间的距离为1200千米和特快列车走完全程的时间,就可以求出特快列车的速度,进而求出高铁列车的速度而得出C的坐标,由待定系数法求出结论.
解:由函数图象得:甲、乙两地之间的距离为1200千米,
特快列车速度为:1200÷12=100(千米/时),
高铁列车与特快列车的速度和为1200÷3=400(千米/时),
高铁列车的速度为:400﹣100=300(千米/时),
∴高铁列车走完全程时间为1200÷300=4(小时),
∴高铁列车到达时是在它俩相遇之后的1小时后,此时高铁列车与特快列车相距400千米,
∴C(4,400).
设线段CD的解析式为y=kx+b(k≠0,k、b为常数),
把(4,400),(12,1200)代入y=kx+b 中,有
![]() 解得
解得![]()
∴y=100x![]() .
.
故答案为:y=100x![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.
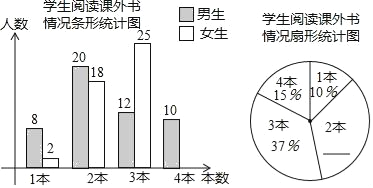
请根据图中信息解决下列问题:
(1)共有 名同学参与问卷调查;
(2)补全条形统计图和扇形统计图;
(3)全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】跳远运动员李阳对训练效果进行测试.6次跳远的成绩如下:7.5,7.7,7.6,7.7,7.9,7.8(单位:m)这六次成绩的平均数为7.7m,方差为
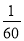 .如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”).
.如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图矩形ABCD中AB=6,AD=4,点P为AB上一点,把矩形ABCD沿过P点的直线l折叠,使D点落在BC边上的D′处,直线l与CD边交于Q点.
(1)在图(1)中利用无刻度的直尺和圆规作出直线l.(保留作图痕迹,不写作法和理由)
(2)若PD′⊥PD,①求线段AP的长度;②求sin∠QD′D.

-
科目: 来源: 题型:
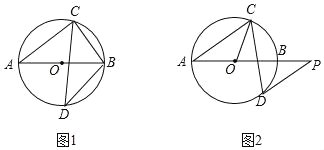
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=
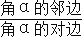 =
=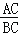 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

-
科目: 来源: 题型:
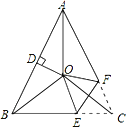
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB的垂直平分线OD交于点O.连接OB、OC,将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
相关试题

