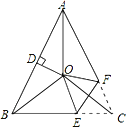
【题目】如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB的垂直平分线OD交于点O.连接OB、OC,将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
参考答案:
【答案】96
【解析】
根据角平分线的定义求出∠BAO,根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到OA=OB,得到∠ABO=∠BAO,证明△AOB≌△AOC,根据全等三角形的性质、折叠的性质、三角形内角和定理计算,得到答案.
解:∵∠BAC=48°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×48°=24°,
×48°=24°,
∵AB=AC,
∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣48°)=66°,
(180°﹣48°)=66°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=24°,
∴∠OBC=∠ABC﹣∠ABO=66°﹣24°=42°,
在△AOB和△AOC中,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴∠OCB=∠OBC=42°,
由折叠的性质可知,OE=CE,
∴∠COE=∠OCB=42°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣42°﹣42°=96°,
故答案为:96.
-
科目: 来源: 题型:
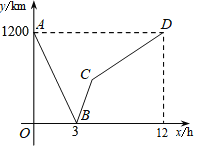
查看答案和解析>>【题目】一列高铁列车从甲地匀速驶往乙地,一列特快列车从乙地匀速驶往甲地,两车同时出发,设特快列车行驶的时间为x(单位:时),特快列车与高铁列车之间的距离为y(单位:千米),y与x之间的函数关系如图所示,则图中线段CD所表示的y与x之间的函数关系式是_____.
-
科目: 来源: 题型:
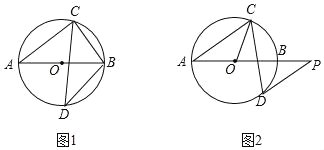
查看答案和解析>>【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=
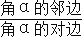 =
=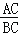 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800
1600
B地区
1600
1200
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种原料,运往A地和B地销售.如表记录的是该产品运往A地和B地供应量y1(kg)、y2(kg)与销售价格x(元)之间的关系:
销售价格x(元)
100
150
200
300
运往A地y1(kg)
300
250
200
100
运往B地y2(kg)
450
350
250
n
(1)请认真分析上表中所给数据,用你所学过的函数来表示其变化规律,并验证你的猜想,分别求出y1与x、y2与x的函数关系式;
(2)用你求出的函数关系式完成上表,直接写出n= ;
(3)直接写出销售价格在 元时,该产品运往A地的供应量等于运往B地的供应量.
相关试题

