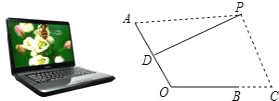
【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ,
, ![]() )
)
参考答案:
【答案】(1)27cm;(2)位置上升了.34.7cm.
【解析】试题分析:(1)连结PO.先由线段垂直平分线的性质得出PO=PA=45cm,则OC=OB+BC=12+24=36cm,然后利用勾股定理即可求出PC=![]() =27cm;(2)过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6
=27cm;(2)过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,则FC=DE=6
DO=6,则FC=DE=6![]() ,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×
,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×![]() =14
=14![]() ,则PC=PF+FC=14
,则PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68>27,即可得出结论.
≈34.68>27,即可得出结论.
试题解析:(1)当PA=45cm时,连结PO.如图:
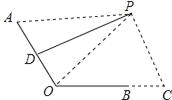 ∵D为AO的中点,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=
∵D为AO的中点,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=![]() =27cm;(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,如图:
=27cm;(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,如图:
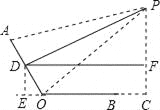 ,则四边形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=
,则四边形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=![]() AO=12,
AO=12,
∴DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,∴FC=DE=6
DO=6,∴FC=DE=6![]() ,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×
,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×![]() =14
=14![]() ,∴PC=PF+FC=14
,∴PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68cm>27cm,∴点P在直线PC上的位置上升了.
≈34.68cm>27cm,∴点P在直线PC上的位置上升了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】建桥中学有A、B两台速印机.用于印刷学习资料和考试试卷,该校七年级举行期末考试,其数学试卷如果用速印机A、B单独印刷,分别需要50分钟和40分钟,在考试时为了保密需要.不能过早提前印刷试卷,决定在考试前由两台速印机同时印刷.在印刷20分钟后B机出现故障.此时离发卷还有10分钟,请你算一算,如果由A机单独完成剩余的印刷任务,会不会影响按时发卷?为什么?(要求列一元一次方程解应用题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
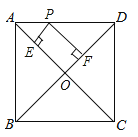
A.2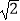
B.4
C.4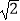
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.
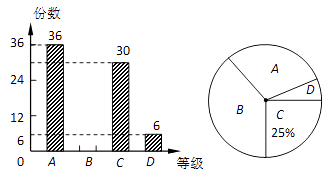
(1)抽取了份作品;
(2)此次抽取的作品中等级为B的作品有份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:18﹣(﹣12)+(﹣15)﹣6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下. -
科目: 来源: 题型:
查看答案和解析>>【题目】同一平面内,不重合的三条直线的交点个数是_____________.
相关试题

