【题目】在直角坐标系xOy中，定义点C（a，b）为抛物线L：y=ax2+bx（a≠0）的特征点坐标．

（1）已知抛物线L经过点A（﹣2，﹣2）、B（﹣4，0），求出它的特征点坐标；

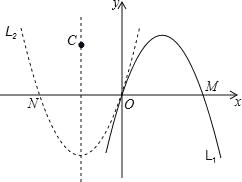
（2）若抛物线L1：y=ax2+bx的位置如图所示：

①抛物线L1：y=ax2+bx关于原点O对称的抛物线L2的解析式为 ；

②若抛物线L1的特征点C在抛物线L2的对称轴上，试求a、b之间的关系式；

③在②的条件下，已知抛物线L1、L2与x轴有两个不同的交点M、N，当一点C、M、N为顶点构成的三角形是等腰三角形时，求a的值．

参考答案：

【答案】（1）（，2）；（2）①y=﹣ax2+bx．②b=2a2．③﹣或﹣．

【解析】

试题分析：（1）结合点A、B点的坐标，利用待定系数法即可求出抛物线L的函数解析式，再结合特征点的定义，即可得出结论；（2）①由抛物线L1：y=ax2+bx与抛物线L2关于原点O对称，可将y换成﹣y，将x换成﹣x，整理后即可得出结论；②根据抛物线L2的解析式可找出它的对称轴为：x=，由抛物线L1的特征点C在抛物线L2的对称轴上可得出a=，变形后即可得出结论；③结合②的结论，表示出点C、M、N三点的坐标，由两点间的距离公式可得出MN、MC、NC的长度，结合等腰三角形的性质分三种情况考虑，分别根据线段相等得出关于a的一元四次方程，解方程再结合a的范围即可得出a的值．

试题解析：（1）将点A（﹣2，﹣2）、B（﹣4，0）代入到抛物线解析式中，得，解得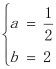：．∴抛物线L的解析式为y=+2x，∴它的特征点为（，2）．（2）①∵抛物线L1：y=ax2+bx与抛物线L2关于原点O对称，∴抛物线L2的解析式为﹣y=a（﹣x）2+b（﹣x），即y=﹣ax2+bx．故答案为：y=﹣ax2+bx．②∵抛物线L2的对称轴为直线：x=﹣=．∴当抛物线L1的特征点C（a，b）在抛物线L2的对称轴上时，有a=，∴a与b的关系式为b=2a2．③∵抛物线L1、L2与x轴有两个不同的交点M、N，∴在抛物线L1：y=ax2+bx中，令y=0，即ax2+bx=0，解得：x1=﹣，x2=0（舍去），即点M（﹣，0）；在抛物线L2：y=﹣ax2+bx中，令y=0，即﹣ax2+bx=0，解得：x1=，x2=0（舍去），即点N（，0）．∵b=2a2，∴点M（﹣2a，0），点N（2a，0），点C（a，2a2）．∴MN=2a﹣（﹣2a）=4a，MC=，NC=．因此以点C、M、N为顶点的三角形是等腰三角形时，有以下三种可能：（1）MC=MN，此时有： =4a，即9a2+4a4=16a2，解得：a=0，或a=±，∵a＜0，∴a=﹣；（2）NC=MN，此时有： =4a，即a2+4a4=16a2，解得：a=0，或a=±，∵a＜0，∴a=﹣；（3）MC=NC，此时有： =，即9a2=a2，解得：a=0，又∵a＜0，∴此情况不存在．综上所述：当以点C、M、N为顶点的三角形是等腰三角形时，a的值为﹣或﹣．

关闭