【题目】已知二次函数y=x2-mx+m-2的图象与x轴有( )个交点.
A. 1个 B. 2个 C. 无交点 D. 无法确定
参考答案:
【答案】B
【解析】
根据一元二次方程x2-mx+m-2=0的根的判别式的符号进行判定二次函数y=x2-mx+m-2的图象与x轴交点的个数.
二次函数y=x2-mx+m-2的图象与x轴交点的纵坐标是零,即当y=0时,x2-mx+m-2=0,
∵△=(-m)2-4(m-2)=(m-2)2+4>0,
∴一元二次方程x2-mx+m-2=0有两个不相等是实数根,即二次函数y=x2-mx+m-2的图象与x轴有2个交点.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(a-b)2-(3-b)(a+b)+2(a-2b)(a+2b),其中a,b满足a2+4a+4+|b-3|=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆西站铁路综合交通枢纽(简称“重庆西站”)自1月25日开通以来,第一个月累计到发旅客2272000人次,实现安全、平稳、有序运行,经受了首场春运“大考”,将数字2272000用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
(1)已知抛物线L经过点A(﹣2,﹣2)、B(﹣4,0),求出它的特征点坐标;
(2)若抛物线L1:y=ax2+bx的位置如图所示:
①抛物线L1:y=ax2+bx关于原点O对称的抛物线L2的解析式为 ;
②若抛物线L1的特征点C在抛物线L2的对称轴上,试求a、b之间的关系式;
③在②的条件下,已知抛物线L1、L2与x轴有两个不同的交点M、N,当一点C、M、N为顶点构成的三角形是等腰三角形时,求a的值.
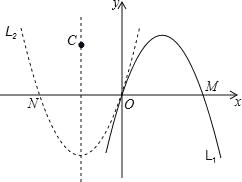
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的盒子中装有9个白球和1个黑球,它们除了颜色外都相同.从中任意摸出一球,则下列叙述正确的是( ).
A.摸到白球是必然事件B.摸到黑球是必然事件
C.摸到白球是随机事件D.摸到黑球是不可能事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长分别为7、11,那么第三边的长可以是( )
A.2
B.3
C.4
D.5
相关试题

