搜索
【题目】已知a、b、c为△ABC的三边长，且a2+b2=6a+10b﹣34，其中c是△ABC中最长的边长，且c为整数，求c的值．
参考答案：
【答案】c=5.6.7
【解析】分析：由a2+b2=6a+10b﹣34，通过配方法求得a，b的值，然后利用三角形的三边关系求得c的取值范围即可．
详解：∵a2+b2=6a+10b﹣34∴a2﹣6a+9+b2﹣10b+25=0
∴（a﹣3）2+（b﹣5）2=0
∴a=3，b=5
∴5﹣3＜c＜5+3
即 2＜c＜8． 又∵c是△ABC中最长的边长
∴c=5.6.7
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P关于x轴对称点P＇的坐标为（4，－5），那么点P关于y轴对称点P＇＇的坐标为（ ）
A.（4，5）
B.（4，－5）
C.（－4，5）
D.（－4，－5） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），对称轴为x=1，给出四个结论：①b2-4ac＞0；②2a+b=0；③a+b=0；④当x=-1或x=3时，函数y的值都等于0，其中正确结论是（ ）
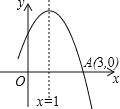
A．②③④ B．①③④ C．①②③ D．①②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，真命题的个数有（ ）
①如果两条直线都与第三条直线平行，那么这两条直线也互相平行．
②过直线外一点有且只有一条直线与这条直线平行．
③两条直线被第三条直线所截，同旁内角互补．
④内错角相等，两直线平行．
A. 4 B. 3 C. 2 D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个三角形三个内角度数的比是2∶3∶4，那么这个三角形是____三角形。
-
科目： 来源： 题型：
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度，随机抽取了部分学生进行调查（每人限选1项），现将调查结果绘制成如下两幅不完整的统计图，根据图中所给的信息解答下列问题．
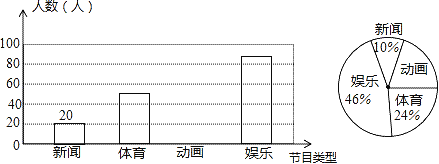
（1）喜爱动画的学生人数和所占比例分别是多少？
（2）请将条形统计图补充完整；
（3）若该校共有学生1000人，依据以上图表估计该校喜欢体育的人数约为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，双曲线y=
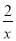（x＞0）经过四边形OABC的顶点A、C，∠ABC=90°，OC平分OA与x轴正半轴的夹角，AB∥x轴．将△ABC沿AC翻折后得△AB′C，B′点落在OA上，则四边形OABC的面积是 ．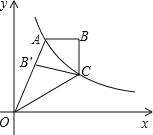
相关试题
