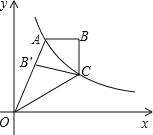
【题目】如图,双曲线y=![]() (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
参考答案:
【答案】2.
【解析】
试题解析:延长BC,交x轴于点D,
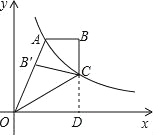
设点C(x,y),AB=a,
∵OC平分OA与x轴正半轴的夹角,
∴CD=CB′,△OCD≌△OCB′,
再由翻折的性质得,BC=B′C,
∵双曲线![]() (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C,
∴S△OCD=![]() xy=1,
xy=1,
∴S△OCB′=![]() xy=1,
xy=1,
由翻折变换的性质和角平分线上的点到角的两边的距离相等可得BC=B′C=CD,
∴点A、B的纵坐标都是2y,
∵AB∥x轴,
∴点A(x-a,2y),
∴2y(x-a)=2,
∴xy-ay=1,
∵xy=2
∴ay=1,
∴S△ABC=![]() ay=
ay=![]() ,
,
∴SOABC=S△OCB′+S△AB'C+S△ABC=1+![]() +
+![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c为△ABC的三边长,且a2+b2=6a+10b﹣34,其中c是△ABC中最长的边长,且c为整数,求c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是____三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
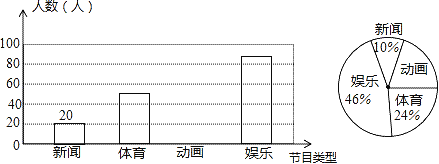
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,分别连接A1B2,连接A2B3….若OA1=a,从左往右的阴影面积依次记作S1、S2、S3…Sn.则Sn= .
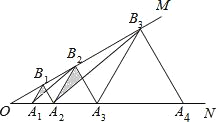
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长是12,一边长是3,求三边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果为x6的是( )
A. x7﹣xB. x2+x4C. (x4)2D. x7÷x
相关试题

