Question

【题目】已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．

（1）如图1，若点P在线段AB的延长线上，求证：EA=EC；

（2）若点P在线段AB上．

①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；

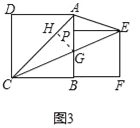
②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．

Answer 1

【答案】（1）证明见解析；（2）①△ACE是直角三角形；②a：b=：1，∠AEC=45°．

【解析】

试题分析：（1）根据正方形的性质和全等三角形的判定定理证明△APE≌△CFE，根据全等三角形的性质证明结论；

（2）①根据正方形的性质、等腰直角三角形的性质解答；

②根据PE∥CF，得到，代入a、b的值计算求出a：b，根据角平分线的判定定理得到∠HCG=∠BCG，证明∠AEC=∠ACB，即可求出∠AEC的度数．

试题解析：（1）∵四边形ABCD和四边形BPEF是正方形，∴AB=BC，BP=BF，∴AP=CF，在△APE和△CFE中，∵AP=CF，∠P=∠F，PE=EF，∴△APE≌△CFE，∴EA=EC；

（2）①∵P为AB的中点，∴PA=PB，又PB=PE，∴PA=PE，∴∠PAE=45°，又∠DAC=45°，∴∠CAE=90°，即△ACE是直角三角形；

②∵EP平分∠AEC，EP⊥AG，∴AP=PG=a﹣b，BG=a﹣（2a﹣2b）=2b﹣a

∵PE∥CF，∴，即，解得：；

作GH⊥AC于H，∵∠CAB=45°，∴HG=AG==，又BG=2b﹣a=，∴GH=GB，GH⊥AC，GB⊥BC，∴∠HCG=∠BCG，∵PE∥CF，∴∠PEG=∠BCG，∴∠AEC=∠ACB=45°，∴a：b=：1；∴∠AEC=45°．