【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C. 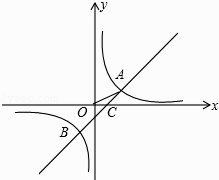
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
参考答案:
【答案】
(1)解:设一次函数解析式为y1=kx+b(k≠0);反比例函数解析式为y2= ![]() (a≠0),
(a≠0),
∵将A(2,1)、B(﹣1,﹣2)代入y1得: ![]() ,
,
∴ ![]() ,
,
∴y1=x﹣1;
∵将A(2,1)代入y2得:a=2,
∴ ![]() ;
;
答:反比例函数的解析式是y2= ![]() ,一次函数的解析式是y1=x﹣1
,一次函数的解析式是y1=x﹣1
(2)解:∵y1=x﹣1,
当y1=0时,x=1,
∴C(1,0),
∴OC=1,
∴S△AOC= ![]() ×1×1=
×1×1= ![]() .
.
答:△AOC的面积为 ![]()
【解析】(1)设一次函数解析式为y1=kx+b(k≠0);反比例函数解析式为y2= ![]() (a≠0),将A(2,1)、B(﹣1,﹣2)代入y1得到方程组
(a≠0),将A(2,1)、B(﹣1,﹣2)代入y1得到方程组 ![]() ,求出即可;将A(2,1)代入y2得出关于a的方程,求出即可;(2)求出C的坐标,根据三角形的面积公式求出即可.
,求出即可;将A(2,1)代入y2得出关于a的方程,求出即可;(2)求出C的坐标,根据三角形的面积公式求出即可.
【考点精析】掌握确定一次函数的表达式和三角形的面积是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
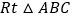 中,
中, ,
, 为
为 边上的中线,
边上的中线,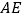 ∥
∥ ,且
,且 ,连接
,连接 .
.(1)求证:四边形
 为菱形;
为菱形;(2)连接
 ,若
,若 平分
平分 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题:
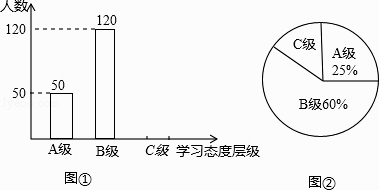
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近80000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于第一、三象限内的
的图像交于第一、三象限内的 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 在
在 轴负半轴上,
轴负半轴上, ,且四边形
,且四边形 是平行四边形,点
是平行四边形,点 的纵坐标为
的纵坐标为 .
.(1)求该反比例函数和一次函数的表达式;
(2)连接
 ,求
,求 的面积;
的面积;(3)直接写出关于
 的不等式
的不等式 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝元旦,某校组织大合唱汇演.初一(1)、(2)班学生准备统一购买服装参加演出(一人买一套),这两班共有学生104名学生参加演出,其中(1)班人数较少,不足50人.下面是某服装厂给出的服装价格表:
购买服装的套数
1﹣50套
51﹣100套
100套以上
每套服装的价格
130元
110元
90元
经估算,如果两个班都以班为单位购买服装,那么一共应付12400元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购买服装,可省多少钱?
(3)如果(2)班不购买了,只有(1)班单独购买,作为组织者的你将如何购买才最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的顶点
的顶点 、
、 分别在
分别在 、
、 轴的正半轴上,点
轴的正半轴上,点 在反比例函数
在反比例函数 的第一象限内的图像上,
的第一象限内的图像上, ,
, ,动点
,动点 在
在 轴的上方,且满足
轴的上方,且满足 .
.(1)若点
 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点 的坐标;
的坐标;(2)连接
 、
、 ,求
,求 的最小值;
的最小值;(3)若点
 是平面内一点,使得以
是平面内一点,使得以 、
、 、
、 、
、 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点 的坐标.
的坐标.
-
科目: 来源: 题型:
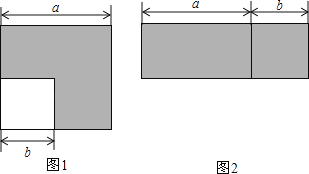
查看答案和解析>>【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
相关试题

