【题目】(1)如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,则阴影部分的面积为 (写成两数平方差的形式);若将图1中的剩余纸片沿线段AB剪开,再把剪成的两张纸片拼成如图2的长方形,则长方形的面积是 (写成两个多项式相乘的形式);比较两图阴影部分的面积,可以得到一个公式: ;
(2)由此可知,通过图形的拼接可以验证一些等式.现在给你两张边长为a的正方形纸片、三张长为a,宽为b的长方形纸片和一张边长为b的正方形纸片(如图3所示),请你用这些纸片拼出一个长方形(所给纸片要用完),并写出它所验证的等式: .

参考答案:
【答案】(1)a2-b2,(a+b)(a-b),(a+b)(a-b)=a2-b2 ;(2)(2a+b)(a+b)=2a2+3ab+b2 ,图见解析.
【解析】
(1)利用正方形的面积公式即可求.根据各边长组合,即可求长方形面积.利用平方差公式即可解答.
(2)根据给出的纸片,利用公式和(1)中的经验即可解答.
(1)a2-b2 (a+b)(a-b) (a+b)(a-b)=a2-b2
(2)(2a+b)(a+b)=2a2+3ab+b2 画图:
-
科目: 来源: 题型:
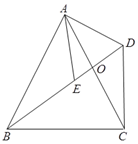
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )

A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论: ①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
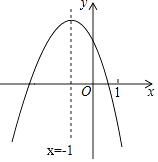
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-
 .
.∴x=-
 是方程2x3-x2+m=0的解. ∴2×(-
是方程2x3-x2+m=0的解. ∴2×(- )3-(-
)3-(- )2+m=0,即-
)2+m=0,即-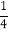 -
-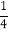 +m=0. ∴m=
+m=0. ∴m= .
.(1)若多项式x2+px-6分解因式的结果中有因式x-3,则实数p= ;
(2)若多项式x3+5x2+7x+q分解因式的结果中有因式x+1,求实数q的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为
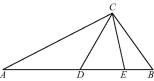
A. 20° B. 25° C. 30° D. 40°
-
科目: 来源: 题型:
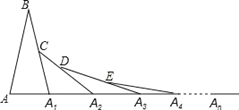
查看答案和解析>>【题目】在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,第n个三角形的以An为顶点的内角的度数为______.
相关试题

