搜索
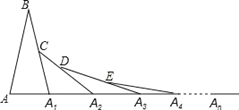
【题目】在第1个△ABA1中，∠B＝20°，AB＝A1B，在A1B上取一点C，延长AA1到A2，使得A1A2＝A1C；在A2C上取一点D，延长A1A2到A3，使得A2A3＝A2D；…，按此做法进行下去，第n个三角形的以An为顶点的内角的度数为______．
参考答案：
【答案】（
）n﹣180°
【解析】
先根据等腰三角形的性质求出∠BA1A的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1，∠DA3A2及∠EA4A3的度数，找出规律即可得出第n个三角形的以An为顶点的内角的度数．
∵在△ABA1中,∠B=20°,AB=A1B，
∴∠BA1A=
==80°，
∵A1A2=A1C,∠BA1A是△A1A2C的外角，
∴∠CA2A1=∠BA1A=×80°=40°；
同理可得，
∠DA3A2=20°,∠EA4A3=10°，
∴第n个三角形的以An为顶点的内角的度数=（）n﹣180°.
故答案为（）n﹣180°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图1，从边长为a的正方形纸片中剪去一个边长为b的小正方形，则阴影部分的面积为 (写成两数平方差的形式)；若将图1中的剩余纸片沿线段AB剪开，再把剪成的两张纸片拼成如图2的长方形，则长方形的面积是 (写成两个多项式相乘的形式)；比较两图阴影部分的面积，可以得到一个公式： ；
(2)由此可知，通过图形的拼接可以验证一些等式．现在给你两张边长为a的正方形纸片、三张长为a，宽为b的长方形纸片和一张边长为b的正方形纸片(如图3所示)，请你用这些纸片拼出一个长方形(所给纸片要用完)，并写出它所验证的等式： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面例题的解法，然后解答问题：
例：若多项式2x3-x2+m分解因式的结果中有因式2x+1，求实数m的值.
解：设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0，则2x+1=0或A=0.
由2x+1=0，解得x=-
.∴x=-
是方程2x3-x2+m=0的解. ∴2×(-)3-(-)2+m=0，即-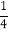
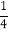-+m=0. ∴m=.(1)若多项式x2+px-6分解因式的结果中有因式x-3，则实数p= ；
(2)若多项式x3+5x2+7x+q分解因式的结果中有因式x+1，求实数q的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为
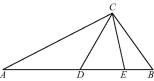
A. 20° B. 25° C. 30° D. 40°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形AOBC的两边在坐标轴上，D是OB的中点，直线CD的函数关系式为y=2x﹣6，则△CDE的面积为 ． （平方单位）
-
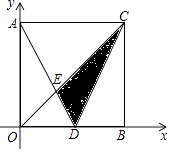
科目： 来源： 题型：
查看答案和解析>>【题目】根据图形填空：
(1)若直线ED，BC被直线AB所截，则∠1和__________是同位角.
(2)若直线ED，BC被直线AF所截，则∠3和__________是内错角.
(3)∠1和∠3是直线AB，AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________，__________被直线BC所截构成的__________角.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线AB∥DF，∠D+∠B=180°，
（1）求证：DE∥BC；
（2）如果∠AMD=75°，求∠AGC的度数．
相关试题
