【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8. 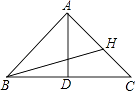
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
参考答案:
【答案】
(1)解:∵AD是BC边上的中线,
∴BD=DC=6.
在△ABD中,BD2+AD2=62+82=102=AB2,
∴△ABD为直角三角形.
∴∠ADB=90°.
∴AD⊥BC.
∵AD⊥BC,BD=DC,
∴AB=AC.
∴△ABC为等腰三角形.
(2)解:∵AH+BH+CH=AC+BH=10+BH,
∴当BH最小时,AH+BH+CH有最小值.
由垂线段的性质可知当BH⊥AC时,BH有最小值.
∴ ![]() BHAC=
BHAC= ![]() BCAD,即
BCAD,即 ![]() ×10BH=
×10BH= ![]() ×12×8,
×12×8,
解得:BH=9.6.
∴AH+BH+CH的最小值=10+9.6=19.6.
【解析】(1)由三角形的中线的定义可知BD=DC=6,然后依据勾股定理的逆定理可证明△ABD为直角三角形,故此AD⊥BC,则AD为BC的垂直平分线,依据线段垂直平分线的性质可知AB=AC;(2)由题意可得到CH+AC=AC=10,故此当BH最小时,AH+BH+CH有最小值,依据垂线段的性质可知当BH⊥AC时,BH有最小值,在△ABC中,依据面积法可求得BH的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
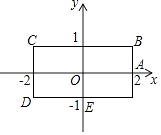
A.(1,﹣1)
B.(2,0)
C.(﹣1,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是长方形,△DCE是等边三角形,A(0,0),B(4,0),D(0,2),求E点的坐标.
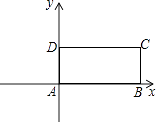
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.

(1)求点B的坐标;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为7?若存在,请直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= , y= , 并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3a2a2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为4,点A和圆心O的距离为3,则点A与⊙O的位置关系是
A.点A在⊙O内B.点A在⊙O上C.点A在⊙O外D.不能确定
相关试题

