Question

【题目】如图1，二次函数y= x2﹣2x+1的图象与一次函数y=kx+b（k≠0）的图象交于A，B两点，点A的坐标为（0，1），点B在第一象限内，点C是二次函数图象的顶点，点M是一次函数y=kx+b（k≠0）的图象与x轴的交点，过点B作轴的垂线，垂足为N，且S△AMO：S四边形AONB=1：48．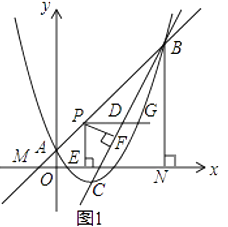

（1）求直线AB和直线BC的解析式；
（2）点P是线段AB上一点，点D是线段BC上一点，PD∥x轴，射线PD与抛物线交于点G，过点P作PE⊥x轴于点E，PF⊥BC于点F．当PF与PE的乘积最大时，在线段AB上找一点H（不与点A，点B重合），使GH+ BH的值最小，求点H的坐标和GH+ BH的最小值；
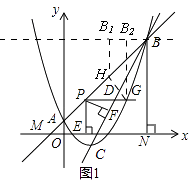
（3）如图2，直线AB上有一点K（3，4），将二次函数y= x2﹣2x+1沿直线BC平移，平移的距离是t（t≥0），平移后抛物线上点A，点C的对应点分别为点A′，点C′；当△A′C′K是直角三角形时，求t的值．

Answer 1

【答案】
（1）解：∵点C是二次函数y= x2﹣2x+1图象的顶点，

∴C（2，﹣1），

∵AO⊥x轴，BN⊥x轴，

∴△MAO∽△MBN，

∵S△AMO：S四边形AONB=1：48，

∴S△AMO：S△BMN=1：49，

∴OA：BN=1：7，

∵OA=1

∴BN=7，

把y=7代入二次函数解析式y= x2﹣2x+1中，可得7= x2﹣2x+1，

∴x1=﹣2（舍），x2=6

∴B（6，7），

∵A的坐标为（0，1），

∴直线AB解析式为y=x+1，

∵C（2，﹣1），B（6，7），

∴直线BC解析式为y=2x﹣5．

（2）解：如图1，

设点P（x0，x0+1），

∴D（ ，x0+1），

∴PE=x0+1，PD=3﹣ x0，

∵∠DPF固定不变，

∴PF：PD的值固定，

∴PE×PF最大时，PE×PD也最大，

PE×PD=（x0+1）（3﹣ x0）=﹣ x02+ x0+3，

∴当x0= 时，PE×PD最大，

即：PE×PF最大．此时G（5， ）

∵△MNB是等腰直角三角形，

过B作x轴的平行线，

∴ BH=B1H，

GH+ BH的最小值转化为求GH+HB1的最小值，

∴当GH和HB1在一条直线上时，GH+HB1的值最小，

此时H（5，6），最小值为7﹣ =

（3）解：令直线BC与x轴交于点I，

∴I（ ，0）

∴IN= ，IN：BN=1：2，

∴沿直线BC平移时，横坐标平移m时，纵坐标则平移2m，平移后A′（m，1+2m），C′（2+m，﹣1+2m），

∴A′C′2=8，A′K2=5m2﹣18m+18，C′K2=5m2﹣22m+26，

当∠A′KC′=90°时，A′K2+KC′2=A′C′2，解得m= ，此时t= m=2 ± ；

当∠KC′A′=90°时，KC′2+A′C′2=A′K2，解得m=4，此时t= m=4 ；

当∠KA′C′=90°时，A′C′2+A′K2=KC′2，解得m=0，此时t=0

【解析】（1）根据S△AMO：S△BMN=1：49可推出OA：BN=1：7，进而算出B（6，7），利用待定系数法求出解析式；（2）最值问题的解决思路就是构建函数，用x的代数式表示PE×PD，GH+ BH的最小值转化为求GH+HB1的最小值;（3）△A′C′K是直角三角形可分类讨论:1.∠A′KC′=90°;2.∠KC′A′=90°;3.∠KA′C′=90°.