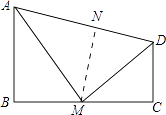
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证: 
(1)AM⊥DM;
(2)M为BC的中点.
参考答案:
【答案】
(1)解:∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM
(2)解:作NM⊥AD交AD于N,
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
【解析】(1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校篮球集训队11名队员进行定点投篮训练,将11名队员在1分钟内投进篮筐的球数由小到大排序后为6,7,8,9,9,9,9,10,10,10,12,这组数据的众数和中位数分别是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A.众数
B.中位数
C.平均数
D.极差 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.对顶角相等
B.某人的体温为100℃是不可能事件
C.同旁内角互补
D.一组邻边相等的平行四边形是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年四月北京很多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰。据测定,杨絮纤维的直径约为0.000 010 5米,将0.000 010 5用科学记数法可表示为( )
A.1.05×105
B.1.05×10-5
C.0.105×10-4
D.10.5×10-6 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图
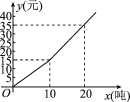
(1)求a的值,某户居民上月用水8吨,应收水费多少元;
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
相关试题

