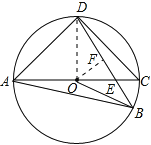
【题目】如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.

(1)求点O到BD的距离及∠OBD的度数;
(2)若DE=2BE,求![]() 的值和CD的长.
的值和CD的长.
参考答案:
【答案】(1)O到BD的距离为1;![]() ;(2)
;(2)![]() ;
;![]()
【解析】
试题(1)作OF⊥BD于点F,连接OD,根据圆周角定理可得出∠DOB=120°,再由OB=OD=![]() AC=2,可得出∠OBD的度数,也可得出OF的长度;
AC=2,可得出∠OBD的度数,也可得出OF的长度;
(2)设BE=2x,则可表示出DF、EF的长度,从而可解出x的值,在RT△OEF中,利用三角函数值的知识可求出∠OED的度数,也可得出cos∠OED的值,判断出DO⊥AC,然后利用等腰直角三角形的性质可得出CD的长度.
(1)作OF⊥BD于点F,连接OD,
∵∠BAD=60°,
∴∠BOD=2∠BAD=120°,
又∵OB=OD,
∴∠OBD=30°,
∵AC为⊙O的直径,AC=4,
∴OB=OD=2.
在Rt△BOF中,∵∠OFB=90°,OB=2,∠OBF=30°,
∴OF=OBsin∠OBF=2sin30°=1,
即点O到BD的距离等于1;
(2)∵OB=OD,OF⊥BD于点F,
∴BF=DF.
由DE=2BE,设BE=2x,则DE=4x,BD=6x,EF=x,BF=3x.
∵BF=OBcos30°![]()
∴![]() ,
,![]()
在Rt△OEF中,∠OFE=90°,∵tan∠OED=![]()
∴∠OED=60°,cos∠OED=![]() ,
,
∴∠BOE=∠OED-∠OBD=30°,
∴∠DOC=∠DOB-∠BOE=90°,
∴∠C=45°
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④
 .其中正确结论的序号是( )
.其中正确结论的序号是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+ ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+ .其中正确结论的序号是 .
.其中正确结论的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国梦”是中华民族每个人的梦,也是每个中小学生的梦.各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符.某中学在全校800名学生中随机抽取部分学生进行调查,调查内容分为四种:
 :非常喜欢,
:非常喜欢, :喜欢,
:喜欢, :一般,
:一般, :不喜欢
:不喜欢被调查的同学只能选取其中的一种.根据调查结果,绘制出两个不完整的统计图(图形如下),并根据图中信息,回答下列问题:

(1)本次调查中,一共调查了多少名学生?
(2)条形统计图中,
 _________,
_________, _____________;
_____________;(3)在扇形统计图中,“
 :喜欢”所在扇形的圆心角的度数是多少?
:喜欢”所在扇形的圆心角的度数是多少?(4)请估计该学校800名学生中“
 :非常喜欢”和“
:非常喜欢”和“ :喜欢”经典诵读的学生共有多少人?
:喜欢”经典诵读的学生共有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:≈1.414,≈1.732)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
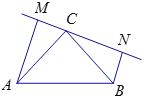
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

相关试题

