搜索
【题目】已知：AD∥BC，AD=CB，AE=CF，请问∠B=∠D吗？为什么？
参考答案：
【答案】∠B=∠D，理由见解析
【解析】试题分析: 由平行线的性质可得∠A=∠C，已知AD=BC，根据等式的性质得AF=CE，从而可根据SAS判定△DAF≌△BCE，根据全等三角形的对应角相等即可求证．
试题解析:∠B=∠D
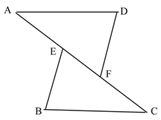
理由是：∵AD∥BC( 已知 )
∴∠A=∠C（ 两直线平行内错角相等。）
∵ AE=CF( 已知 )
∴AE+EF=CF+EF（等式性质）
即AF=CE
在△ADF和△CBE中
AD=CB （已知）
∠A=∠C（已证）
AF=CE（已证）
∴ △AOC≌△BOD （ASA ）
∴ ∠B＝∠D （ 全等三角形对应角相等。）
点睛:此题主要考查学生对全等三角形的判定方法以及全等三角形的性质的立即及运用.
-
科目： 来源： 题型：
查看答案和解析>>【题目】平面上有三个点，以其中两点为端点画线段，共可画__________线段.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个点从数轴的原点开始，先向左移动3个单位长度，再向右移动6个单位长度，这个点最终所对应的数是（ ）
A. +6 B. -3 C. +3 D. -9
-
科目： 来源： 题型：
查看答案和解析>>【题目】倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答
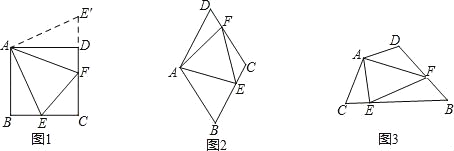
习题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解：
∵正方形ABCD中，AB=AD，∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°-45°=45°=∠EAF．
又∵AE′=AE，AF=AF
∴△AE′FF≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究．
观察分析：
观察图1，由解答可知，该题有用的条件是①．ABCD是四边形，点E、F分别在边BC、CD上；②．AB=AD；③．∠B=∠D=90°∠；④．∠EAF=
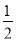∠BAD．类比猜想：
在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
要解决上述问题，可从特例入手，请同学们思考：如图2，在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？试证明．
（2）在四边形ABCD中，点E、F分别在边BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=
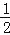∠BAD时，还有EF=BE+DF吗？使用图3证明．归纳概括：
反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，BO平分∠CBA，CO平分∠ACB，过O作EF∥BC，若AB＝12，AC＝8，求△AEF的周长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果 x-y=3，m+n=2，则 ( y + m) -( x - n) 的值是_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将21.54°用度、分、秒表示为 ．
相关试题
