搜索
【题目】如图所示，BO平分∠CBA，CO平分∠ACB，过O作EF∥BC，若AB＝12，AC＝8，求△AEF的周长。
参考答案：
【答案】20
【解析】试题分析：首先根据角平分线的性质以及平行线的性质得出△BEO和△CFO为等腰三角形，从而得出BE=OE，CF=OF，然后根据三角形的周长计算公式将线段进行转换得出三角形的周长.
试题解析：∵BO平分∠CBA，∴∠EBO=∠OBC，∵CO平分∠ACB
∴∠FCO=∠OCB， ∵EF∥BC，∴∠EOB=∠OBC，∠FOC=∠OCB，
∴∠EBO=∠EOB，∠FOC=∠FCO， ∴BE=OE，CF=OF，
∴△AEF的周长AE+OE+OF+AF=AE+BE+CF+AF=AB+AC，
∵AB=12，AC=8， ∴C△AEF=12+8=20．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个点从数轴的原点开始，先向左移动3个单位长度，再向右移动6个单位长度，这个点最终所对应的数是（ ）
A. +6 B. -3 C. +3 D. -9
-
科目： 来源： 题型：
查看答案和解析>>【题目】倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答
习题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．
解：
∵正方形ABCD中，AB=AD，∠BAD=∠ADC=90°
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°-45°=45°=∠EAF．
又∵AE′=AE，AF=AF
∴△AE′FF≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究．
观察分析：
观察图1，由解答可知，该题有用的条件是①．ABCD是四边形，点E、F分别在边BC、CD上；②．AB=AD；③．∠B=∠D=90°∠；④．∠EAF=
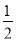∠BAD．类比猜想：
在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
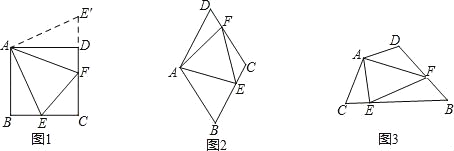
要解决上述问题，可从特例入手，请同学们思考：如图2，在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？试证明．
（2）在四边形ABCD中，点E、F分别在边BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=
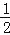∠BAD时，还有EF=BE+DF吗？使用图3证明．归纳概括：
反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：AD∥BC，AD=CB，AE=CF，请问∠B=∠D吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果 x-y=3，m+n=2，则 ( y + m) -( x - n) 的值是_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将21.54°用度、分、秒表示为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】冰冰家新安装了一台太阳能热水器，一天她测量发现18：00时，太阳能热水器水箱内水的温度是80℃，以后每小时下降4℃，第二天，冰冰早晨起来后测得水箱内水的温度为32℃，请你猜一猜她起床的时间是__________________．
相关试题
