【题目】为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水,对居民家庭每户每月用水量采用分档递增收费的方式,每户每月用水量不超过基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为对基本用水量进行决策,随机抽查![]() 户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:
户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:

(1)为确保![]() %的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
%的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
(2)若将(1)中确定的基本用水量及其以内的部分按每立方米![]() 元交费,超过基本用水量的部分按每立方米
元交费,超过基本用水量的部分按每立方米![]() 元交费.设
元交费.设![]() 表示每户每月用水量(单位:
表示每户每月用水量(单位:![]() ),
),![]() 表示每户每月应交水费(单位:元),求
表示每户每月应交水费(单位:元),求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)某户家庭每月交水费是![]() 元,请按以上收费方式计算该家庭当月用水量是多少立方米?
元,请按以上收费方式计算该家庭当月用水量是多少立方米?
参考答案:
【答案】(1)38m3;(2)![]()
![]() ;(3)43.
;(3)43.
【解析】
试题分析:(1)根据统计表可得出月均用水量不超过38吨的居民户数占2000户的70%,由此即可得出结论;
(2)分0≤x≤38及x>38两种情况,找出y与x的函数关系式;
(3)求出当x=38时的y值,与80.9比较后可得出该家庭当月用水量超出38立方米,令y=2.5x﹣26.6=80.9求出x值即可.
试题解析:(1)200+160+180+220+240+210+190=1400(户),
2000×70%=1400(户),
∴基本用水量最低应确定为多38m3.
答:为确保70%的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为38立方米.
(2)设x表示每户每月用水量(单位:m3),y表示每户每月应交水费(单位:元),
当0≤x≤38时,y=1.8x;
当x>38时,y=1.8×38+2.5(x﹣38)=2.5x﹣26.6.
综上所述:y与x的函数关系式为![]()
![]() .
.
(3)∵1.8×38=68.4(元),68.4<80.9,
∴该家庭当月用水量超出38立方米.
当y=2.5x﹣26.6=80.9时,x=43.
答:该家庭当月用水量是43立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形
B.五边形
C.六边形
D.七边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中是勾股数的是( )
A. 4,5,6 B. 0.3,0.4,0.5 C. 1,2,3 D. 5,12,13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是ABCD对角线AC上两点,且AE=CF.
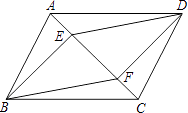
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?
(3)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=3,xy=1,则x2+y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法把367 060精确到十位,并用科学记数法表示为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段a=4,b=1,如果线段c是线段a、b的比例中项,那么c=_____.
相关试题

