【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.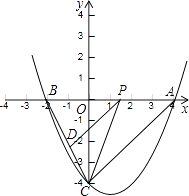
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
参考答案:
【答案】
(1)解:由题意,得 ![]() ,
,
解得  ,
,
∴抛物线的解析式为y= ![]() ﹣x﹣4
﹣x﹣4
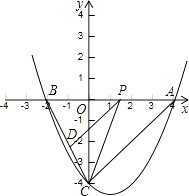
(2)解:设点P运动到点(x,0)时,有BP2=BDBC,
令x=0时,则y=﹣4,
∴点C的坐标为(0,﹣4).
∵PD∥AC,
∴△BPD∽△BAC,
∴ ![]() .
.
∵BC= ![]() =
= ![]() =2
=2 ![]() ,
,
AB=6,BP=x﹣(﹣2)=x+2.
∴BD= ![]() =
= ![]() =
= ![]() .
.
∵BP2=BDBC,
∴(x+2)2= ![]() ×2
×2 ![]() ,
,
解得x1= ![]() ,x2=﹣2(﹣2不合题意,舍去),
,x2=﹣2(﹣2不合题意,舍去),
∴点P的坐标是( ![]() ,0),即当点P运动到(
,0),即当点P运动到( ![]() ,0)时,BP2=BDBC
,0)时,BP2=BDBC
(3)解:∵△BPD∽△BAC,
∴ ![]() ,
,
∴ ![]() ×
× ![]()
S△PDC=S△PBC﹣S△PBD= ![]() ×(x+2)×4﹣
×(x+2)×4﹣ ![]()
∵ ![]() ,
,
∴当x=1时,S△PDC有最大值为3.
即点P的坐标为(1,0)时,△PDC的面积最大.
【解析】(1)利用待定系数法把AB坐标代入解析式即可;(2)先由PD∥AC可得△BPD∽△BAC,得出比例式,用x的式子表示BD,代入到 BP2=BDBC
求出x;(3)用作差法表示△PCD的面积,即S△PDC=S△PBC﹣S△PBD,构建出二次函数,用配方法求出最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年9月29日,由北京外交人员服务局主办、北京外交人员房屋服务公司、北京市乒乓球运动协会承办的首届中外外交官“友谊杯”乒乓球赛在北京齐家园外交公寓体育运动中心举办,为了纪念这次活动,某校开展了乒乓球知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其成绩如图所示:

 根据上图填写下表:
根据上图填写下表:平均数
中位数
众数
甲班

______

乙班
______
8
______
 已知甲班5名同学成绩的方差是
已知甲班5名同学成绩的方差是 ,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定?
,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯
一户居民每月用电量x(单位:度)
电费价格(单位:元/度)
一档
0<x≤180
a
二档
180<x≤280
b
三档
x>280
0.82
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红购买了两次笔记本,购买情况及总费用如下表
购买次数
购买各种笔记本的数量
 单位:本
单位:本
购买总费用
 单位:元
单位:元
甲
乙
第一次
1
4
22
第二次
2
3
24
 备注:两次购买甲、乙笔记本的单价不变
备注:两次购买甲、乙笔记本的单价不变
 甲、乙笔记本的单价分别是多少元?
甲、乙笔记本的单价分别是多少元? 小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本?
小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )﹣3﹣20160﹣|﹣5|;
)﹣3﹣20160﹣|﹣5|;(2)(3a2)2﹣a22a2+(﹣2a3)2+a2;
(3)(x+5)2﹣(x﹣2)(x﹣3);
(4)(2x+y﹣2)(2x+y+2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人利用不同的交通工具,沿同一路线从A地出发到距离A地350千米的B地办事,甲先出发,乙后出发,甲、乙两人距A地的路程和时间的关系如图所示,根据图示提供的信息解答:
 乙比甲晚______小时出发;乙出发______小时后追上甲;
乙比甲晚______小时出发;乙出发______小时后追上甲; 分别求甲、乙两人离开A地的路程s关于t的函数关系式;
分别求甲、乙两人离开A地的路程s关于t的函数关系式; 求乙比甲早几小时到达B地?
求乙比甲早几小时到达B地?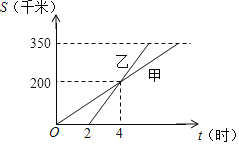
相关试题

