【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).

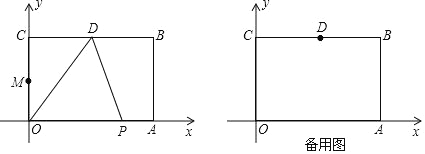
(1)①点D的坐标是(___,___)；

②当点P在AB上运动时,点P的坐标是(___,___)(用t表示)；

(2)写出△POD的面积S与t之间的函数关系式，并求出△POD的面积等于9时点P的坐标；

(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)

参考答案：

【答案】（1）①D(3,4)；② P(6, t6)；（2），当P(4.5,0)或(6,2)时，△POD的面积为9；（3）4.

【解析】

(1)①利用矩形的性质求出B、C两点坐标,再利用中点坐标公式计算即可;

②点P在线段AB上,求出PA即可;

(2)分三种情形分别讨论求解即可;

(3)根据,构建方程即可解决问题

(1)①∵四边形OABC是矩形,A(6,0),B(6,4)，

∴C(0,4)，

∵D是BC的中点，

∴D(3,4).

②当P在AB上运动时,P(6,t6)，

故答案为3，4，6，t6；

(2)①当0<t6时,P(t,0)，

S=×t×4=2t.

②当6<t10时，

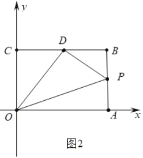
S=S矩形OCBAS△OPAS△PBDS△CDO=2412×6×(t6)12×3×(10t)6=t+21，

③当10<t<13时,P(16t,4)，PD=13t，

∴S=×(13t)×4=2t+26，

综上所述,.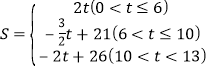

若S=9，由①得到2t=9，t=4.5，

∴P1(4.5,0)，

若S=9,由②得到,t+21=9，即t=8，

∴P2(6,2).

若S=9,由③得到,2t+26=9,t=(不合题意舍弃)，

综上所述,当P(4.5,0)或(6,2)时，△POD的面积为9.

(3)如图4中，

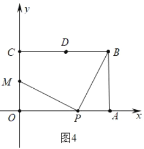
∵OM=CM=2，PM=PB，OP=t，

∴22+t2=42+(6t)2，

解得t=4.

∴将线段BP绕点P逆时针旋转，点B恰好落到OC的中点M处，则此时点P运动的时间t=4s，

故答案为4.

关闭