【题目】已知:在Rt△ABC中,∠C=90°,sinA、sinB是方程x2+px+q=0的两个根.
(1)求实数p、q应满足的条件
(2)若p、q满足(1)的条件,方程x2+px+q=0的两个根是否等于Rt△ABC中两锐角A、B的正弦?
参考答案:
【答案】
(1)
解:∵sinA、sinB是方程x2+px+q=0的两个根,∴sinA+sinB=﹣p,即:sinA+cosA=﹣p,∴![]() sin(A+45°)=﹣p
sin(A+45°)=﹣p
∵0°<A<90°,∴1<﹣p≤![]() ,∴﹣
,∴﹣![]() ≤p<﹣1,∵sinAsinB=q,即sinAcosA=q,∴sin2A=2q,∴0<q<
≤p<﹣1,∵sinAsinB=q,即sinAcosA=q,∴sin2A=2q,∴0<q<![]() ,
,
∵sin2A+sinB2=(sinA+sinB)2﹣2sinAsinB,∴p2﹣2q=1,
∴实数p、q应满足的条件是:p2﹣2q=1,∴﹣![]() ≤p<﹣1,0<q≤
≤p<﹣1,0<q≤![]() .
.
(2)
解:∵0<q≤![]() ,设sin2A=2q,则2A=2a,或180°﹣2a,即:A=a或90°﹣a,
,设sin2A=2q,则2A=2a,或180°﹣2a,即:A=a或90°﹣a,
∵sina和sin(90°﹣a)是方程的两根,即它们是直角三角形的两个锐角的正弦值.
【解析】(1)根据sinA+cosA=![]() sin(A+45°),sinAcosA=
sin(A+45°),sinAcosA=![]() sin2A,以及根与系数的关系,即可得到关于p,q的不等式,以及sin2A+sinB2=1,即可求得p,q的关系.
sin2A,以及根与系数的关系,即可得到关于p,q的不等式,以及sin2A+sinB2=1,即可求得p,q的关系.
(2)根据(1)可以得到sin2A=2q,求得A的值,证明A的值可以取互余的两个角的度数,即可证得.
【考点精析】认真审题,首先需要了解锐角三角函数的增减性(当角度在0°~90°之间变化时:(1)正弦值随着角度的增大(或减小)而增大(或减小)(2)余弦值随着角度的增大(或减小)而减小(或增大)(3)正切值随着角度的增大(或减小)而增大(或减小)(4)余切值随着角度的增大(或减小)而减小(或增大)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分7分)在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高。

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
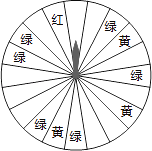
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球.
(1)求摸到的球是白球的概率.
(2)如果要使摸到白球的概率为
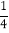 ,需要在这个口袋中再放入多少个白球?
,需要在这个口袋中再放入多少个白球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某个正方体的表面展开图,各个面上分别标有1﹣6的不同数字,若将其折叠成正方体,则相交于同一个顶点的三个面上的数字之和最大的是
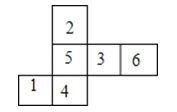
相关试题

