【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
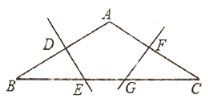
参考答案:
【答案】EG=5cm.
【解析】
连接AE、AG,根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,再根据等腰三角形两底角相等求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEG=60°,同理求出∠AGE=60°,从而判断出,△AEG为等边三角形,再根据等边三角形三边都相等列式求解即可.
如图,连接AE、AG,
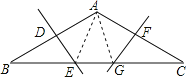
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B=![]() =30°,
=30°,
∴∠BAE=30°,
∴∠AEG=60°,
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG,
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又BE+EG+GC=BC=15(cm),
∴EG=5(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.
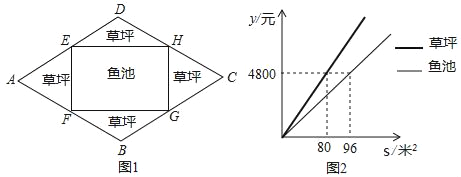
(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300
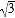 m2,求EF的长度;
m2,求EF的长度;(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
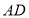 是
是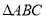 的角平分线,
的角平分线,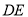 ,
,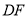 分别是
分别是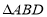 和
和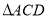 的高,连接
的高,连接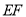 交
交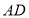 于
于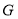 .下列结论:①
.下列结论:①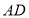 垂直平分
垂直平分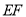 ;②
;②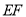 垂直平分
垂直平分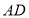 ;③
;③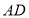 平分
平分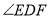 ;④当
;④当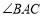 为
为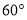 时,
时,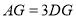 ,其中不正确的结论的个数为( )
,其中不正确的结论的个数为( )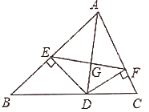
A.
 B.
B.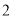 C.
C.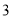 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).

(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且
 ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )

A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

相关试题

