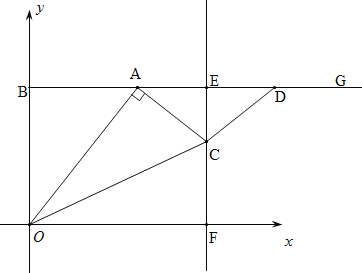
【题目】如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.
(1)用含t的式子表示点E的坐标为_______;
(2)当t为何值时,∠OCD=180°?
(3)当点C与点F不重合时,设△OCF的面积为S,求S与t之间的函数解析式.
参考答案:
【答案】(1)E(![]() ,8);(2)
,8);(2)![]() ;(3)
;(3)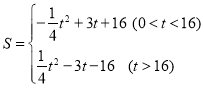 .
.
【解析】
试题分析:(1)由AD=OB=8,得到AE=ED=4,再由点A的横坐标为t,得到点E的坐标;
(2)当∠OCD=180°时,如图1,由EC∥BO,得到![]() ,即EC=
,即EC=![]() ,再由△AEC∽△OBA,得到
,再由△AEC∽△OBA,得到![]() ,从而EC=
,从而EC=![]() ,故
,故![]() =
=![]() ,解方程即可求出t的值;
,解方程即可求出t的值;
(3)当C与F重合时,由(2)得:![]() =8,解得t=16,故分两种情况讨论:①
=8,解得t=16,故分两种情况讨论:①![]() ,②
,②![]() .由于
.由于![]() ,OF=BE=
,OF=BE=![]() ,只需要表示出CF代入公式即可.
,只需要表示出CF代入公式即可.
试题解析:(1)∵AD=OB=8,∴AE=ED=4,∵点A的横坐标为t,∴E(![]() ,8);
,8);
(2)当∠OCD=180°时,如图1,∵EC∥BO,∴![]() ,∴
,∴![]() ,∴EC=
,∴EC=![]() ,∵AC⊥OA,∴∠1+∠2=90°,∵∠2+∠3=90°,∴∠1=∠3,∵∠AEC=∠ABO,∴△AEC∽△OBA,∴
,∵AC⊥OA,∴∠1+∠2=90°,∵∠2+∠3=90°,∴∠1=∠3,∵∠AEC=∠ABO,∴△AEC∽△OBA,∴![]() ,∴
,∴![]() ,∴EC=
,∴EC=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() ,解得:
,解得:![]() 或
或![]() (舍去),∴t=
(舍去),∴t=![]() ;
;

(3)当C与F重合时,由(2)得:![]() =8,解得t=16,∴分两种情况讨论:①
=8,解得t=16,∴分两种情况讨论:①![]() ,②
,②![]() .
.
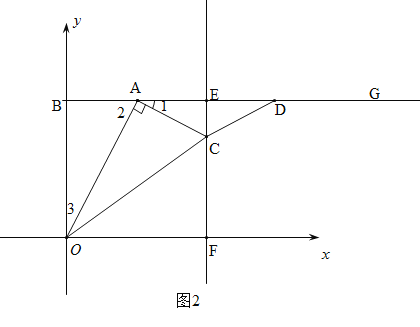
①当![]() 时,如图2,由(2)得:EC=
时,如图2,由(2)得:EC=![]() ,则CF=
,则CF=![]() ,∵OF=BE=
,∵OF=BE=![]() ,∴
,∴![]() ,即
,即![]() ;
;
②当![]() 时,如图3,由(2)得:EC=
时,如图3,由(2)得:EC=![]() ,则CF=
,则CF=![]() ,∵OF=BE=
,∵OF=BE=![]() ,
,
∴![]() ,即
,即![]() ;
;

综上所述: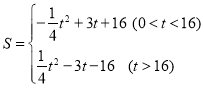 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
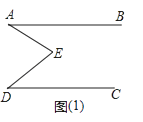
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)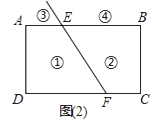
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AH⊥BC于H,E,D,F分别是AB,BC,AC的中点,则四边形EDHF是( )
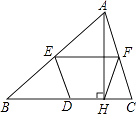
A.一般梯形
B.等腰梯形
C.直角梯形
D.直角等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】双营服装店老板到厂家选购A、B两种型号的服装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元,
(1)求A,B两种型号的服装每件分别多少元?
(2)若销售1件A型服装可获利18元,销售1件B型服装可获利30元,根据市场需求,服装店老板决定,购进A型服装的数量要比购进B型服装数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总的获利不少于699元,问有几种进货方案如何进货? -
科目: 来源: 题型:
查看答案和解析>>【题目】若某人沿坡度ⅰ=3:4的坡度前进10m,则他所在的位置比原来的位置升高 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D -
科目: 来源: 题型:
查看答案和解析>>【题目】如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为( )
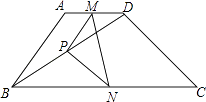
A.4
B.5
C.6
D.7
相关试题

