【题目】如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC= ![]() ,AD=
,AD= ![]() ,求DE的长.
,求DE的长. 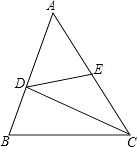
参考答案:
【答案】解:∵BD=1,DC=3,BC= ![]() ,
,
又∵12+32=( ![]() )2,
)2,
∴BD2+CD2=BC2,
∴△BCD是直角三角形且∠BDC=90°,
∴∠ADC=90°,
∴AC= ![]() =4,
=4,
又∵E点为AC的中点
∴DE= ![]() =2.
=2.
【解析】首先根据勾股定理的逆定理判定△BCD是直角三角形且∠BDC=90°,再利用勾股定理可求出AC的长,进而可求出DE的长.
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1) ×
×  ﹣4×
﹣4×  ×(1﹣
×(1﹣  )0
)0
(2)|﹣5|+(π﹣3.1)0﹣( )﹣1+
)﹣1+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在相同的条件下各射靶10次,每次命中的环数如下: 甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,10,6
(1)分别计算甲、乙两组数据的方差;
(2)根据计算结果比较两人的射击水平. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形周长为20,其中一条边长为x,设矩形面积为y
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为55000000千米.用科学记数法表示数据55000000为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
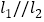 ,直线
,直线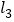 与
与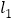 、
、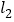 分别交于C、D两点,点P是直线
分别交于C、D两点,点P是直线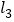 上的一动点.
上的一动点.(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有
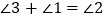 这一相等关系?试说明理由;
这一相等关系?试说明理由;(2)如图,当动点P在线段CD之外且在
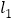 的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;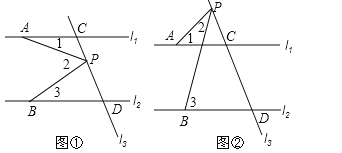
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.

求证:四边形OCED是菱形.
相关试题

