搜索
【题目】计算：（ 
）﹣1﹣（2﹣ 
）0﹣2sin60°+| ﹣2|
参考答案：
【答案】解：（ 
）﹣1﹣（2﹣ 
）0﹣2sin60°+| ﹣2| =2﹣1﹣2× 
+2﹣
=1﹣ +2﹣
=3﹣2
【解析】首先计算乘方和乘法，然后从左向右依次计算，求出算式（ 
）﹣1﹣（2﹣ 
）0﹣2sin60°+| ﹣2|的值是多少即可．
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本，需要知道零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某体育文化用品商店购进篮球和排球共30个，进价和售价如下表，若全部销售完后共可获利润1680元．
篮球
排球
进价（元/个）
150
120
售价（元/个）
200
180
（1）请利用二元一次方程组求购进篮球和排球各多少个？
（2）“双11”快到了，这个体育文化用品商店也准备搞促销活动，计划篮球9折销售，排球8折销售，则销售8个篮球的利润与销售几个排球的利润相等？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程．
已知：如图1，直线l和直线l外一点P．
求作：直线l的平行直线，使它经过点P．
作法：如图2．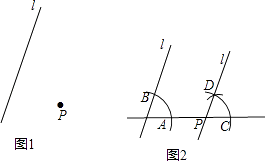
（i）过点P作直线m与直线l交于点O；
（ii）在直线m上取一点A（OA＜OP），以点O为圆心，OA长为半径画弧，与直线l交于点B；
（iii）以点P为圆心，OA长为半径画弧，交直线m于点C，以点C为圆心，AB长为半径画弧，两弧交于点D；
（iv）作直线PD．
所以直线PD就是所求作的平行线．
请回答：该作图的依据是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中,AB=AC,D为BC边的中点,BE平分∠ABC,交AD于E,F为△ABC外一点,且∠ACF=
∠ACB,BE=CF,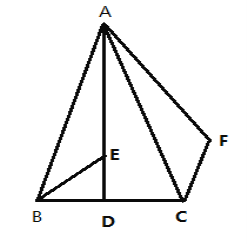
（1）求证：∠BAF=3∠BAD
（2）若DE=5，AE=13，求线段AB的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy，直线y=x﹣1与y轴交于点A，与双曲线y=
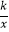交于点B（m，2）．
（1）求点B的坐标及k的值；
（2）将直线AB平移，使它与x轴交于点C，与y轴交于点D，若△ABC的面积为6，求直线CD的表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】一个三位数，若十位上的数字是百位数字与个位数字的和，我们称这个三位数叫“圣诞数”，并且把这个“圣诞数”的前两位组成的两位数记为m，后两位组成的两位数记为n，并规定d=
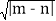。如一个三位数385，
3+5=8，
385是“圣诞数”，且m=38，n=85，则d=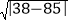
=
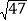.（1）写出最小的“圣诞数”；
（2）求证：任意一个“圣诞数”是11的倍数；
（3）求出所有能被8整除的“圣诞数”，并直接写出这些“圣诞数”中d的最小值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．
（1）求证：CE∥GF；
（2）试判断∠AED与∠D之间的数量关系，并说明理由；
（3）若∠EHF＝80°，∠D＝30°，求∠AEM的度数．
相关试题
