【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
(1)如图①,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图②,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).

参考答案:
【答案】(1)点A’的坐标为(![]() ,1);(2)1;(3)
,1);(2)1;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)因点![]() ,点
,点![]() ,可得OA=
,可得OA=![]() ,OB=1,根据折叠的性质可得△A’OP≌△AOP,由全等三角形的性质可得OA’=OA=
,OB=1,根据折叠的性质可得△A’OP≌△AOP,由全等三角形的性质可得OA’=OA=![]() ,在Rt△A’OB中,根据勾股定理求得
,在Rt△A’OB中,根据勾股定理求得![]() 的长,即可求得点A的坐标;(2)在Rt△AOB中,根据勾股定理求得AB=2,再证△BOP是等边三角形,从而得∠OPA =120°.在判定四边形OPA’B是平行四边形,根据平行四边形的性质即可得
的长,即可求得点A的坐标;(2)在Rt△AOB中,根据勾股定理求得AB=2,再证△BOP是等边三角形,从而得∠OPA =120°.在判定四边形OPA’B是平行四边形,根据平行四边形的性质即可得![]() 的长;
的长;
试题解析:(1)因点![]() ,点
,点![]() ,
,
∴OA=![]() ,OB=1.
,OB=1.
根据题意,由折叠的性质可得△A’OP≌△AOP.
∴OA’=OA=![]() ,
,
由![]() ,得∠A’BO=90°.
,得∠A’BO=90°.
在Rt△A’OB中,![]() ,
,
∴点A’的坐标为(![]() ,1).
,1).
(2) 在Rt△AOB中,OA=![]() ,OB=1,
,OB=1,
∴![]()
∵当![]() 为
为![]() 中点,
中点,
∴AP=BP=1,OP=![]() AB=1.
AB=1.
∴OP=OB=BP,
∴△BOP是等边三角形
∴∠BOP=∠BPO=60°,
∴∠OPA=180°-∠BPO=120°.
由(1)知,△A’OP≌△AOP,
∴∠OPA’=∠OPA=120°,P’A=PA=1,
又OB=PA’=1,
∴四边形OPA’B是平行四边形.
∴A’B=OP=1.
(3)![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
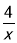 的图象与性质】
的图象与性质】(1)函数y=x+
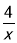 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下列四个函数图象中函数y=x+
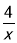 的图象大致是 ;
的图象大致是 ;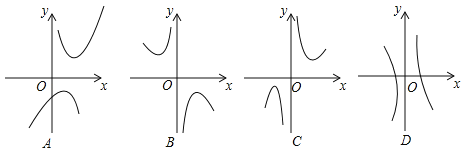
(3)对于函数y=x+
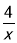 ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0
∴y=x+
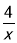 =(
=(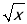 )2+(
)2+(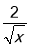 )2=(
)2=(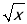 ﹣
﹣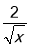 )2+
)2+ ∵(
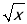 ﹣
﹣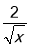 )2≥0
)2≥0∴y≥ .
[拓展运用]
(4)若函数y=
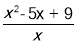 ,则y的取值范围 .
,则y的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
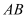 是⊙
是⊙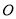 的直径,
的直径,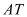 是⊙
是⊙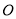 的切线,
的切线,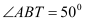 ,
,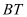 交⊙
交⊙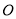 于点
于点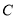 ,
,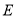 是
是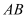 上一点,延长
上一点,延长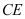 交⊙
交⊙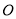 于点
于点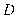 .
.(1)如图①,求
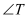 和
和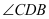 的大小;
的大小;(2)如图②,当
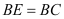 时,求
时,求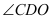 的大小.
的大小.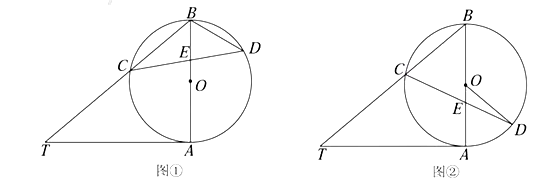
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
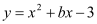 (
( 是常数)经过点
是常数)经过点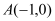 .
.(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,
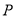 关于原点的对称点为
关于原点的对称点为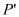 .
.①当点
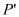 落在该抛物线上时,求
落在该抛物线上时,求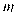 的值;
的值;②当点
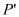 落在第二象限内,
落在第二象限内,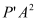 取得最小值时,求
取得最小值时,求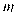 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用
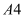 纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为
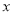 (
(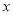 为非负整数).
为非负整数).(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
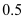
2
…
乙复印店收费(元)
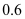
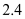
…
(2)设在甲复印店复印收费
 元,在乙复印店复印收费
元,在乙复印店复印收费 元,分别写出
元,分别写出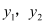 关于
关于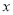 的函数关系式;
的函数关系式;(3)当
 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的第一边长为3a+2b,第二边比第一边长a﹣b,第三边比第二边短2a.请用a、b式子分别表示第二边和第三边,并求这个三角形的周长(最后结果都要求最简)
相关试题

