【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,顶点的坐标为(1,-4);(2)
,顶点的坐标为(1,-4);(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1) 抛物线![]() 经过点
经过点![]() ,代入求得b值即可求得抛物线的解析式,把抛物线化为顶点式,直接写出顶点坐标即可;(2)①由点P(m,t)在抛物线
,代入求得b值即可求得抛物线的解析式,把抛物线化为顶点式,直接写出顶点坐标即可;(2)①由点P(m,t)在抛物线![]() 上,可得
上,可得![]() ,
,
![]() 关于原点的对称点为
关于原点的对称点为![]() ,可得P’(-m,-t),即可得
,可得P’(-m,-t),即可得![]() ,所以
,所以![]() ,解方程即可求得m的值;②构造
,解方程即可求得m的值;②构造![]() 与t的二次函数模型,根据二次函数的性质求得
与t的二次函数模型,根据二次函数的性质求得![]() 的值最小是t的值,再代入二次函数
的值最小是t的值,再代入二次函数![]() 中求得m的值即可.
中求得m的值即可.
试题解析:(1)∵抛物线![]() 经过点
经过点![]() ,
,
∴0=1-b-3,解得b=-2.
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴顶点的坐标为(1,-4).
(2)①由点P(m,t)在抛物线![]() 上,有
上,有![]() .
.
∵![]() 关于原点的对称点为
关于原点的对称点为![]() ,有P’(-m,-t).
,有P’(-m,-t).
∴![]() ,即
,即![]()
∴![]()
解得![]()
②由题意知,P’(-m,-t)在第二象限,
∴-m<0,-t>0,即m>0,t<0.
又抛物线![]() 的顶点的坐标为(1,-4),得-4≤t<0.
的顶点的坐标为(1,-4),得-4≤t<0.
过点P’作P’H⊥x轴,H为垂足,有H(-m,0).
又![]() ,
,![]() ,
,
则![]()
当点A和H不重合时,在Rt△P’AH中,![]()
当点A和H重合时,AH=0, ![]() ,符合上式.
,符合上式.
∴![]() ,即
,即![]()
记![]() ,则
,则![]() ,
,
∴当t=-![]() 时,y’取得最小值.
时,y’取得最小值.
把t=-![]() 代入
代入![]() ,得
,得![]()
解得![]()
由m>0,可知![]() 不符合题意
不符合题意
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
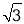 ).
).(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
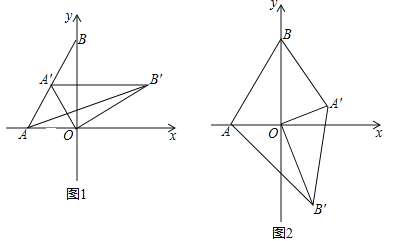
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
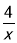 的图象与性质】
的图象与性质】(1)函数y=x+
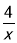 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下列四个函数图象中函数y=x+
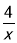 的图象大致是 ;
的图象大致是 ;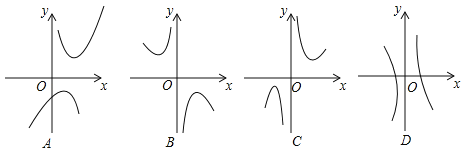
(3)对于函数y=x+
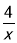 ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0
∴y=x+
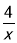 =(
=(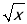 )2+(
)2+(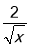 )2=(
)2=(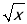 ﹣
﹣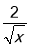 )2+
)2+ ∵(
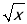 ﹣
﹣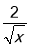 )2≥0
)2≥0∴y≥ .
[拓展运用]
(4)若函数y=
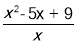 ,则y的取值范围 .
,则y的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
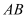 是⊙
是⊙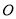 的直径,
的直径,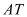 是⊙
是⊙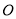 的切线,
的切线,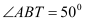 ,
,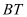 交⊙
交⊙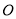 于点
于点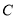 ,
,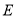 是
是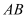 上一点,延长
上一点,延长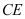 交⊙
交⊙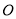 于点
于点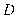 .
.(1)如图①,求
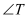 和
和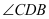 的大小;
的大小;(2)如图②,当
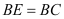 时,求
时,求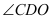 的大小.
的大小.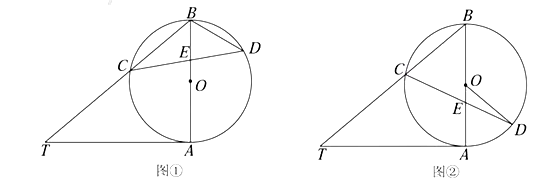
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸片
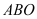 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点 ,点
,点 ,点
,点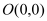 .
.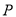 是边
是边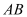 上的一点(点
上的一点(点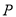 不与点
不与点 重合),沿着
重合),沿着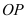 折叠该纸片,得点
折叠该纸片,得点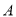 的对应点
的对应点 .
.(1)如图①,当点
 在第一象限,且满足
在第一象限,且满足 时,求点
时,求点 的坐标;
的坐标;(2)如图②,当
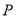 为
为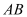 中点时,求
中点时,求 的长;
的长;(3)当
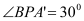 时,求点
时,求点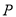 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用
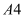 纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为
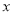 (
(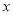 为非负整数).
为非负整数).(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
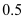
2
…
乙复印店收费(元)
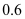
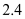
…
(2)设在甲复印店复印收费
 元,在乙复印店复印收费
元,在乙复印店复印收费 元,分别写出
元,分别写出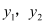 关于
关于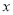 的函数关系式;
的函数关系式;(3)当
 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
相关试题

