【题目】如图, ![]() 为
为 ![]() 的直角边
的直角边 ![]() 上一点,以
上一点,以 ![]() 为半径的
为半径的 ![]() 与斜边
与斜边 ![]() 相切于点
相切于点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.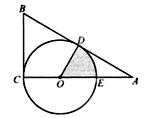
(1)求 ![]() 的长;
的长;
(2)求图中阴影部分的面积.
参考答案:
【答案】
(1)
解:在Rt△ABC中,AB=![]() =
=![]() =2
=2 ![]() .
.
∵BC⊥OC
∴BC是⊙O的切线
又∵AB是⊙O的切线
∴BD=BC=![]()
∴AD=AB-BD=![]()
(2)
解:在Rt△ABC中,sinA= ![]() =
=![]() =
=![]() .
.
∴∠A=30°.
∵AB切⊙O于点D.
∴OD⊥AB.
∴∠AOD=90°-∠A=60°.
∵ ![]() =tanA=tan30°.
=tanA=tan30°.
∴ ![]() =
=![]() .
.
∴OD=1.
S阴影=![]() =
=![]() .
.
【解析】(1)在Rt△ABC中,利用勾股定理求出AB的长,然后根据切线的判定证出BC为切线,然后可根据切线长定理可求解.
(2)在Rt△ABC中,根据∠A的正弦求出∠A度数,然后根据切线的性质求出OD的长,和扇形圆心角的度数,再根据扇形的面积公式可求解.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, OC 是AOB 的平分线, P 是OC 上的一点, PD OA 于 D ,PE OB 于 E . F 是OC 上的另一点,连接 DF 、 EF .
(1)求证: DPF EPF ;
(2)比较 DF 与 EF 的大小关系,并说明理由.
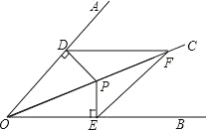
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了
 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):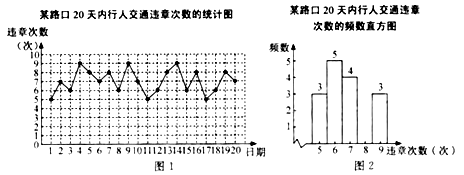
请根据所给信息,解答下列问题:
(1)第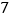 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这  天中,行人交通违章
天中,行人交通违章 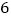 次的有多少天?
次的有多少天?
(2)请把图2中的频数直方图补充完整;
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了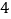 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明对我校七年级(1)班喜欢什么球类运动的调查,下列图形中的左图是小明对所调查结果的条形统计图.
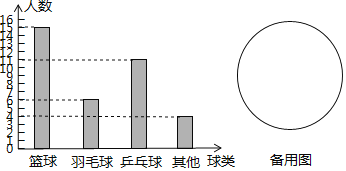
(1)问七年级(1)班共有多少学生?
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动.
(3)从统计图中你可以获得哪些信息?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察一列数:1,2,4,8,16,… 我们发现,这一列数从第二项起,每一项与它前一项的比都等于2. 一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是_________;
(2)如果一列数
 ,
,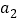 ,
,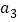 ,
,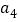 ,...是等比数列,且公比为
,...是等比数列,且公比为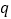 . 那么有:
. 那么有: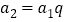 ,
,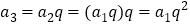 ,
,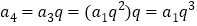 ,则
,则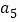 =______ _,
=______ _,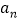 = (用
= (用 与
与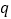 的式子表示);
的式子表示);(3)一个等比数列的第2项是9,第4项是36,求它的公比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, AC BC , BD AD ,垂足分别为C 、D , AC BD , AC 、BD 交于O
(1)求证: CAB DBA ;
(2)求证: SADO SBCO .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形
 的对角线
的对角线  ,
,  相交于点
相交于点  .
.
(1)如图1, ,
,  分别是
分别是  ,
,  上的点,
上的点,  与
与  的延长线相交于点
的延长线相交于点  .若
.若  ,求证:
,求证:  ;
;
(2)如图2, 是
是  上的点,过点
上的点,过点  作
作  ,交线段
,交线段  于点
于点  ,连结
,连结  交
交  于点
于点  ,交
,交  于点
于点  .若
.若  ,
,
①求证: ;
;
②当 时,求
时,求  的长.
的长.
相关试题

