【题目】如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数. 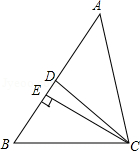
参考答案:
【答案】解:∵CE是AB边上的高, ∴∠A+∠ACE=90°,∠B+∠BCE=90°.
∵CD是∠ACB的角平分线,
∴∠ACD=∠BCD= ![]() ∠ACB,
∠ACB,
又∵∠DCE=10°,∠B=60°,
∴∠BCE=90°﹣∠B=30°,∠BCD=∠BCE+∠DCE=40°,
∴∠ACE=∠ACD+∠DCE=∠BCD+∠DCE=50°,
∴∠A=90°﹣∠ACE=40°.
【解析】在△BCE中由∠BEC=90°,∠B=60°能够得出∠BCE=30°;结合CD是∠ACB的角平分线,∠DCE=10°可得出∠ACE的度数;在Rt△ACE中由∠ACE的度数及∠AEC=90°,即可得出∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠A+∠C=270°,则∠B=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(﹣3,2)重合,则点A的坐标是( )
A.(2,5)
B.(﹣8,5)
C.(﹣8,﹣1)
D.(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果电梯上升5层记为+5.那么电梯下降2层应记为( )
A. +2 B. ﹣2 C. +5 D. ﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
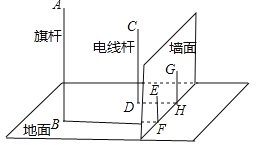
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规在图①中画一个以AB为边的“好玩三角形”;
(2)如图②,在Rt△ABC中,∠C=90°,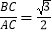 ,求证:△ABC是“好玩三角形”.
,求证:△ABC是“好玩三角形”. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
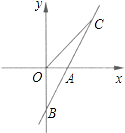
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
相关试题

